AHSEC - Class 12 Question Papers: Mathematics' 2016

2016

MATHEMATICS

Full Marks: 100

Pass Marks: 30

Time: 3 hours

The figures in the margin indicate full marks for the questions

1. Answer the following questions: 1x10=10

1. Let. For, let if and only if. Write down as a subset of.
2. What is the domain of the function?
3. If, find.
4. For what value of, the matrix is not invertible?
5. If A is a square matrix of order 3 such that, find.
6. A function is defined as follows

Which one of the following is true?

1. is continuous at 0 and 1.
2. is continuous at 1 and 2.
3. is continuous at 0 and 2.
4. is continuous at 0, 1 and 2.

7. Which one of the following is true? For the function

1. is strictly decreasing in
2. is strictly increasing in
3. is neither increasing nor decreasing in

8. What is the unit vector along the vector?
9. What are the direction cosines of the normal to plane?
10. What is the equation of the?

2. Show that the relation R in the set Z of integers given by, 3+1

is an equivalence relation. Find the set of all elements related to 0.

Or

A function is defined by, . Examine if 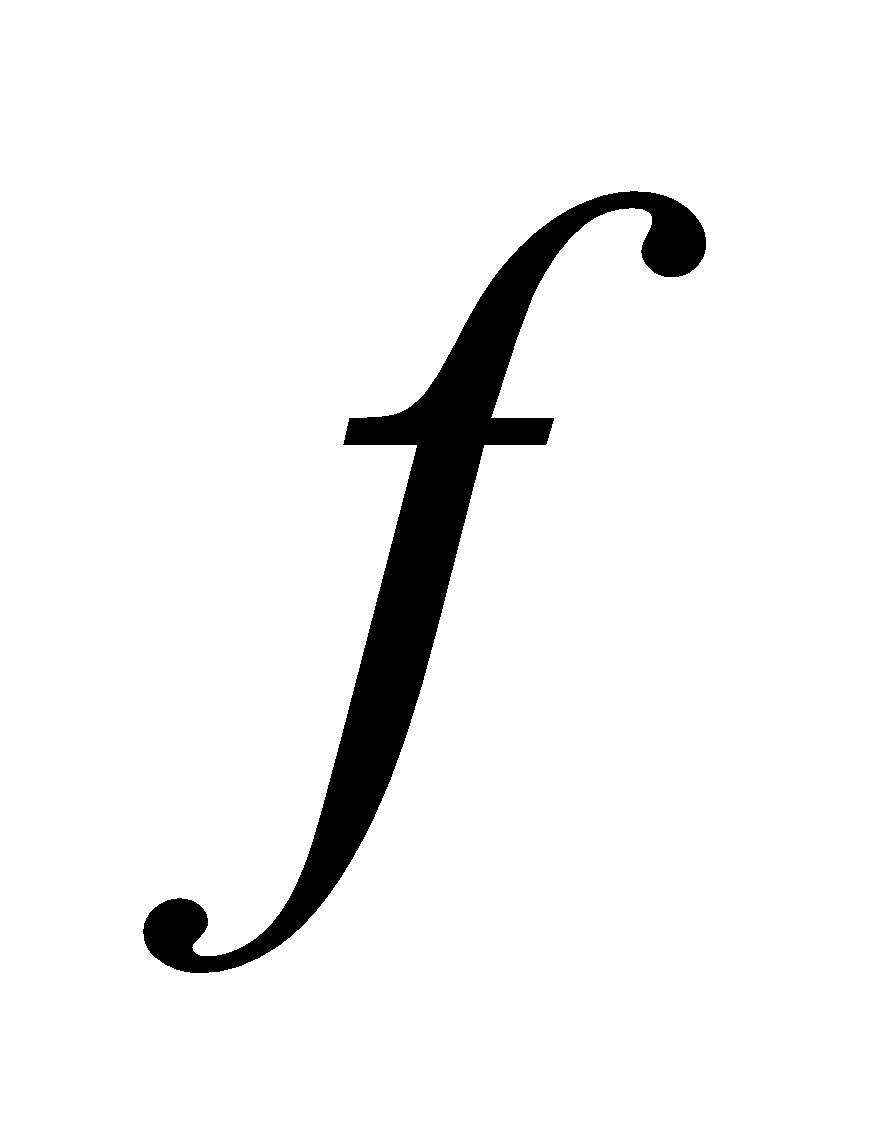is one-one and onto. 2+2

3. If, prove that. 4

Or

Prove that,

4. If, show that . Hence find. 2+2=4

Or

Using elementary row operations, find the inverse of the matrix

5. Show that is continuous but not differentiable at. 2+2=4

Or

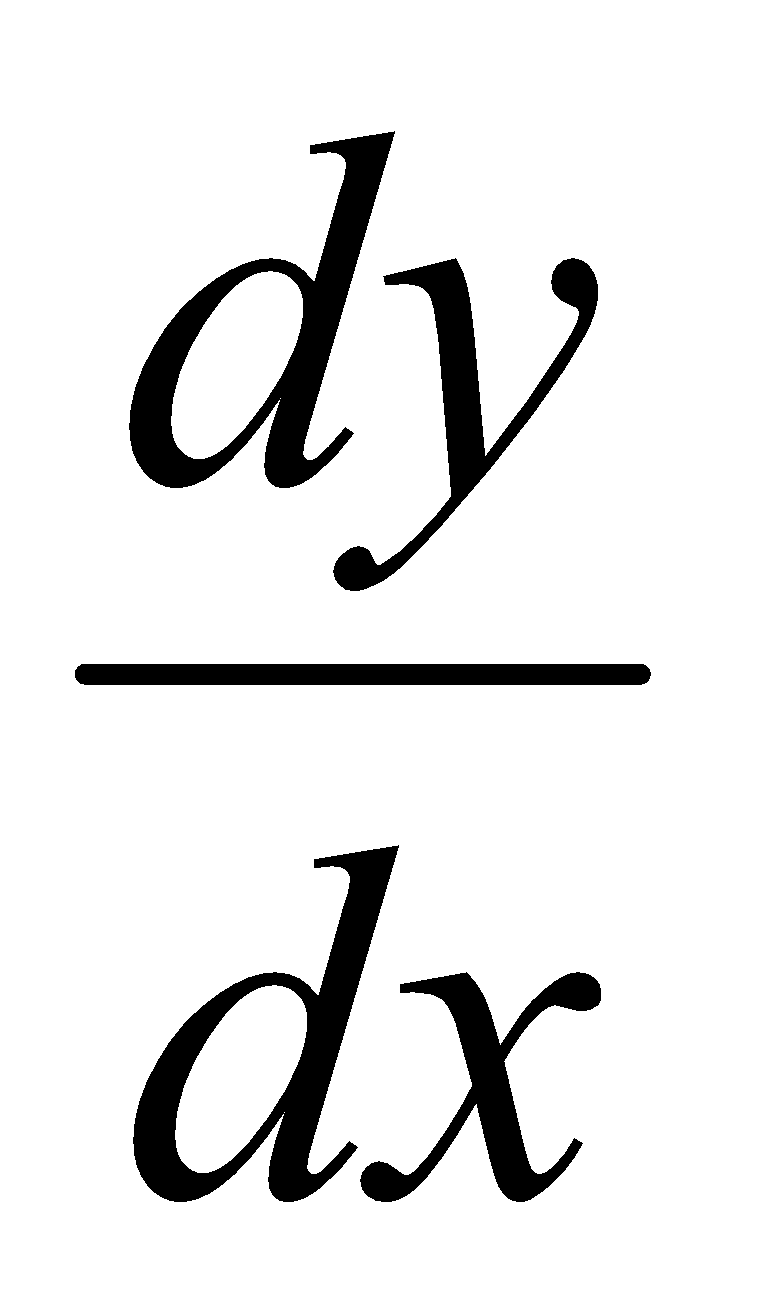If, find. 4

6. Find the point at which the tangent to the curve 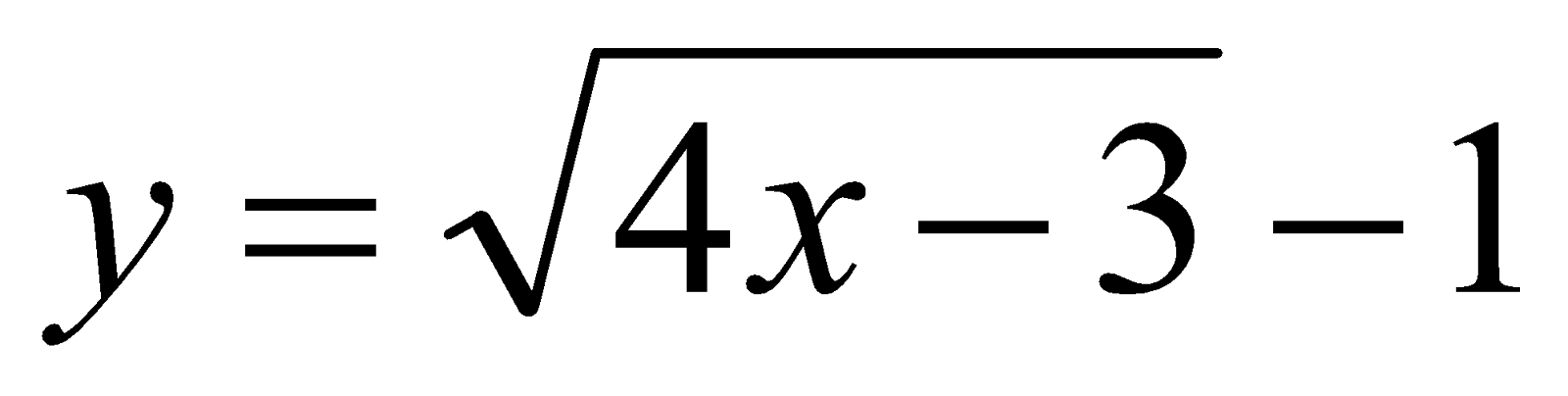has its slope. Also find the equation of the tangent at that point. 2+2=4

Or

State Rolle’s Theorem and verify it for the following function. 1+3=4

7. Evaluate the following integrals: 4x2=8

1. 

Or

2. 

Or

8. Solve: 4

Or

From a differential equation by eliminating the arbitrary constants a and b from 4

9. Show that the family of curves for which the slope of the tangent at any point on its is, is given by. 4

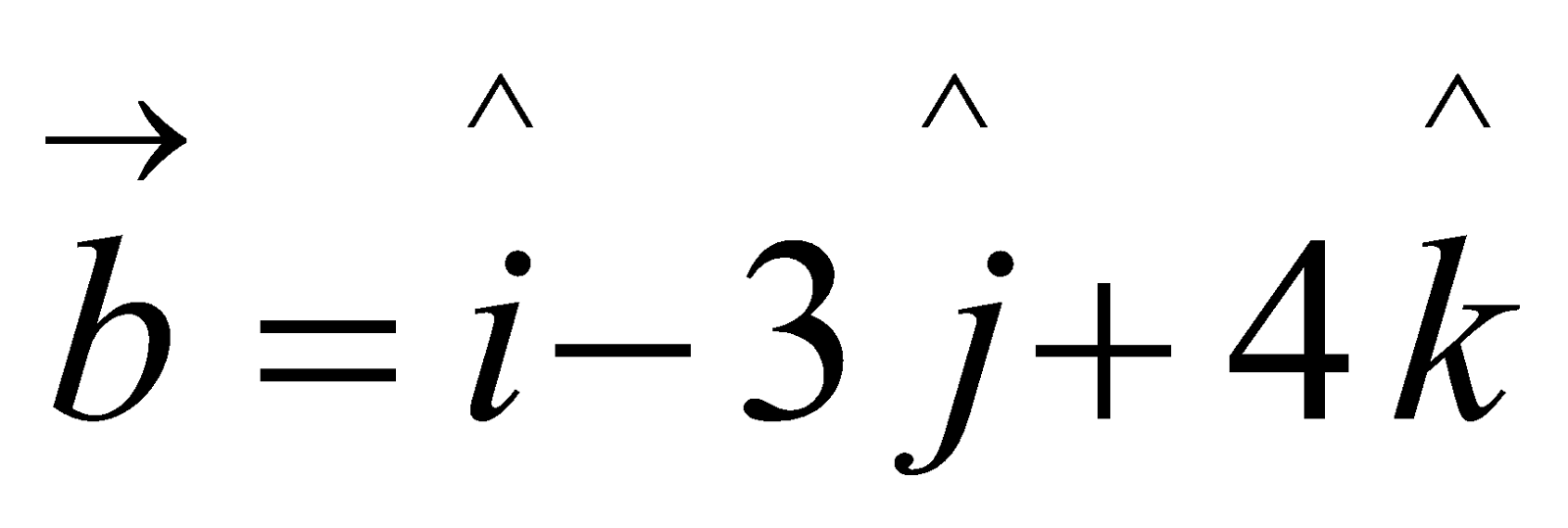10. Find the area of the parallelogram whose diagonals are given by the vectors and. 4

Or

If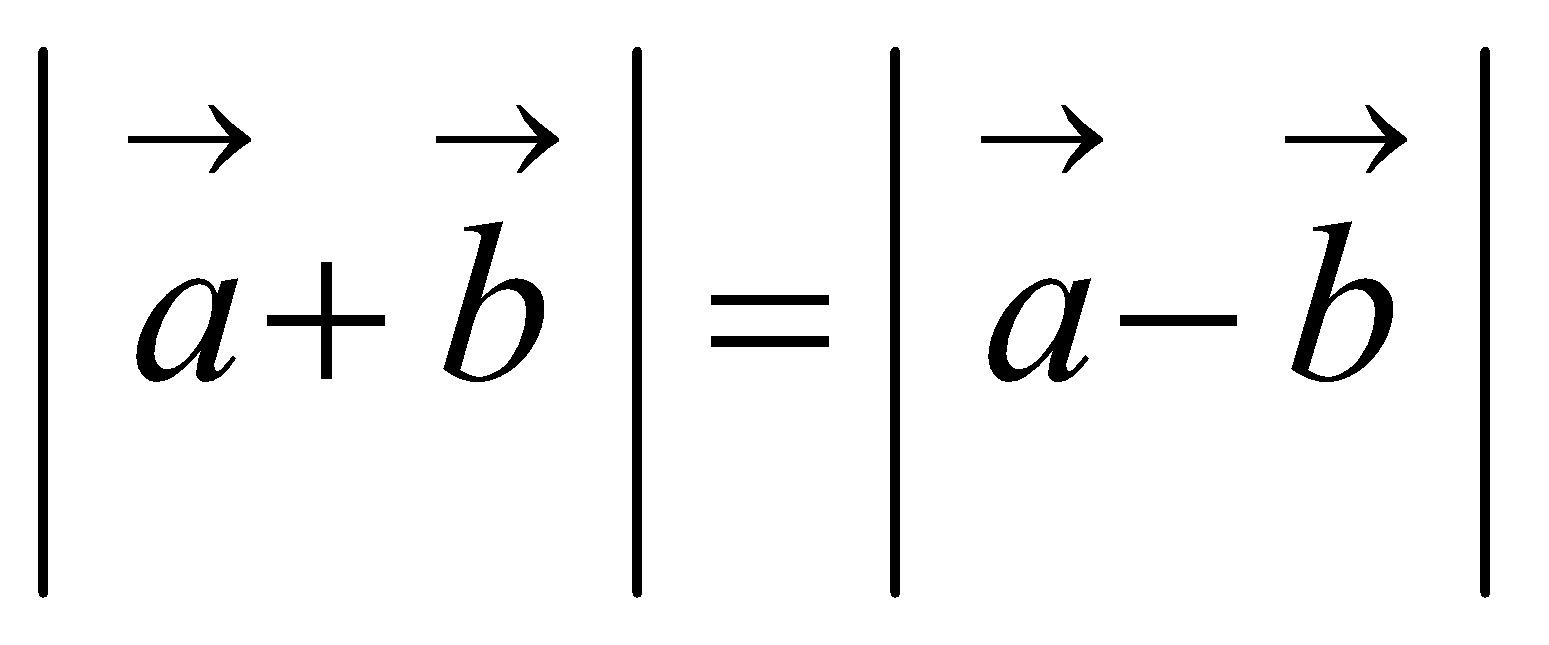, show that and 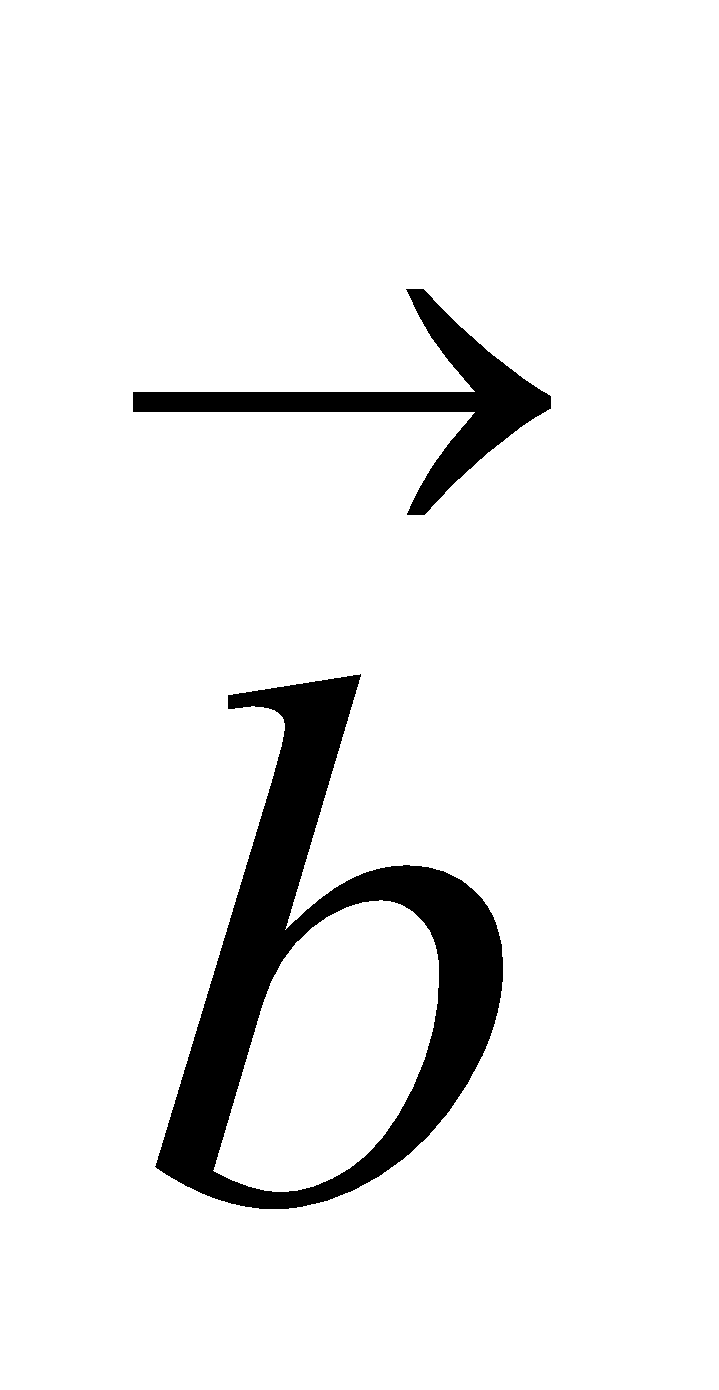are perpendicular to each other. 4

11. Find the shortest distance between the lines whose vector equations are given by

and 4

Or

Find the acute angle between the planes whose vector equations are

And 4

12. Two cards are drawn successively, without replacement from a well-shuffled pack of 52 cards. Find the probability distribution of the number of aces. 4

Or

A box contains 2 told and 3 silver coins. Another box contains 3 gold and 3 silver coins. A box is chosen at random and a coin is drawn from it. If the selected coin is a gold coin, find the probability that it was drawn from the second box. 4

13. Prove that 6

Or

Show that 6

14. Answer any one:

1. Find the maximum and minimum values, if any, of the following functions. 3+3=6

1. 
2. 

2. Find the intervals in which the function is

1. Increasing.
2. Decreasing.

15. Find the area of the region in the first quadrant enclosed by the, the lineand the circle. 6

Or

Find the area of the region common to the two circles and. 6

16. Evaluate as a limit of a sum. 6

17. Find the vector equation of the plane passing through the intersection of the planes and and perpendicular to the vector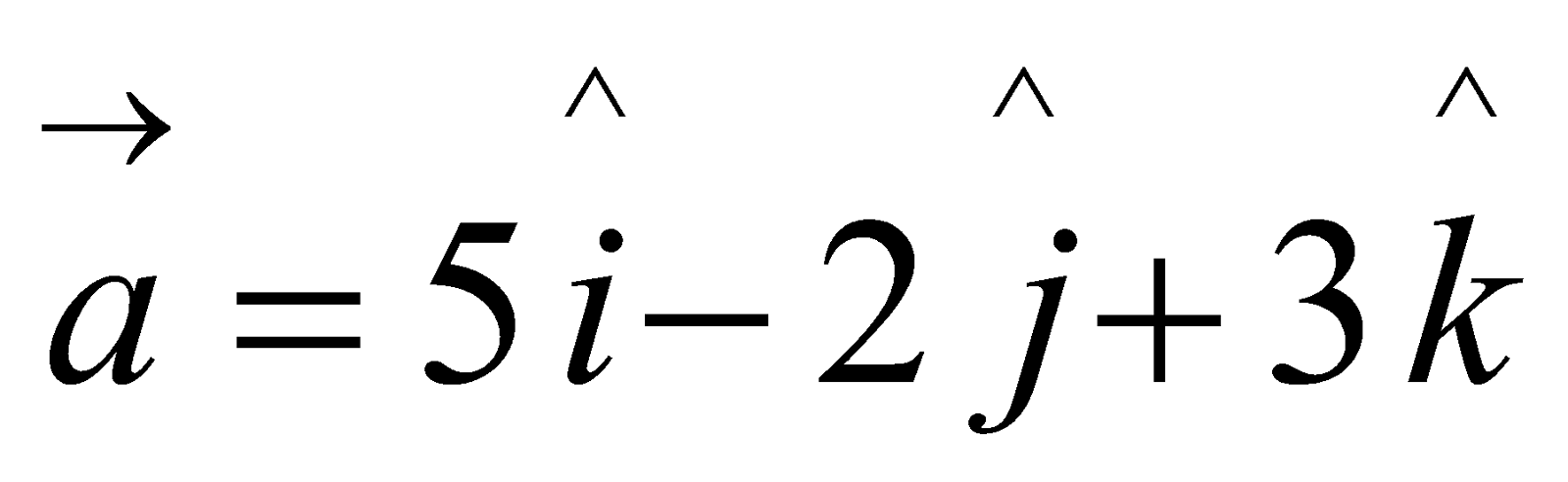. 6

Or

Find the equation of the plane that makes intercepts a, b and c on x, y and z-axes respectively. Also, if p is the length of the normal from the origin to this plane, prove that:- 3+3=6

18. Solve the following linear programming problem graphically. 6

Maximize and minimize

Subject to constraints

Or

Maximize the minimize 6

19. The sum and the product of the mean and variance of a binomial distribution are 24 and 128 respectively. Find the distribution. 6

Or

If a fair coin is tossed 10 times, find the probability of getting 2+2+2=6

1. Exactly six heads.
2. At least six heads.
3. At most six heads.