AHSEC - Class 12 Question Papers: Mathematics'2015;

2015

MATHEMATICS

Full Marks: 100

Pass Marks: 30

Time: 3 hours

The figures in the margin indicate full marks for the questions

1. Answer the following questions: 1x10=10

1. If, what is the number of relations on?
2. Find the principal value of.
3. If, what is the order of the matrix?
4. If is a nonsingular matrix such that, what is?
5. What is the co-factor of 7 in the determinant
6. Is the derivative of an even function even?
7. Is the function increasing?
8. What are the direction cosines of the vector?
9. If the distance of a place from the origin be ‘d’ and direction cosines of the normal to the plane through origin be, what are the co-ordinates of the foot of the normal?
10. What are the equations of the planes parallel to and at a distance ‘a’ from it?

2. A function is defined by . Is the function one-one, and onto? Justify your answer. 2+2=4

Or

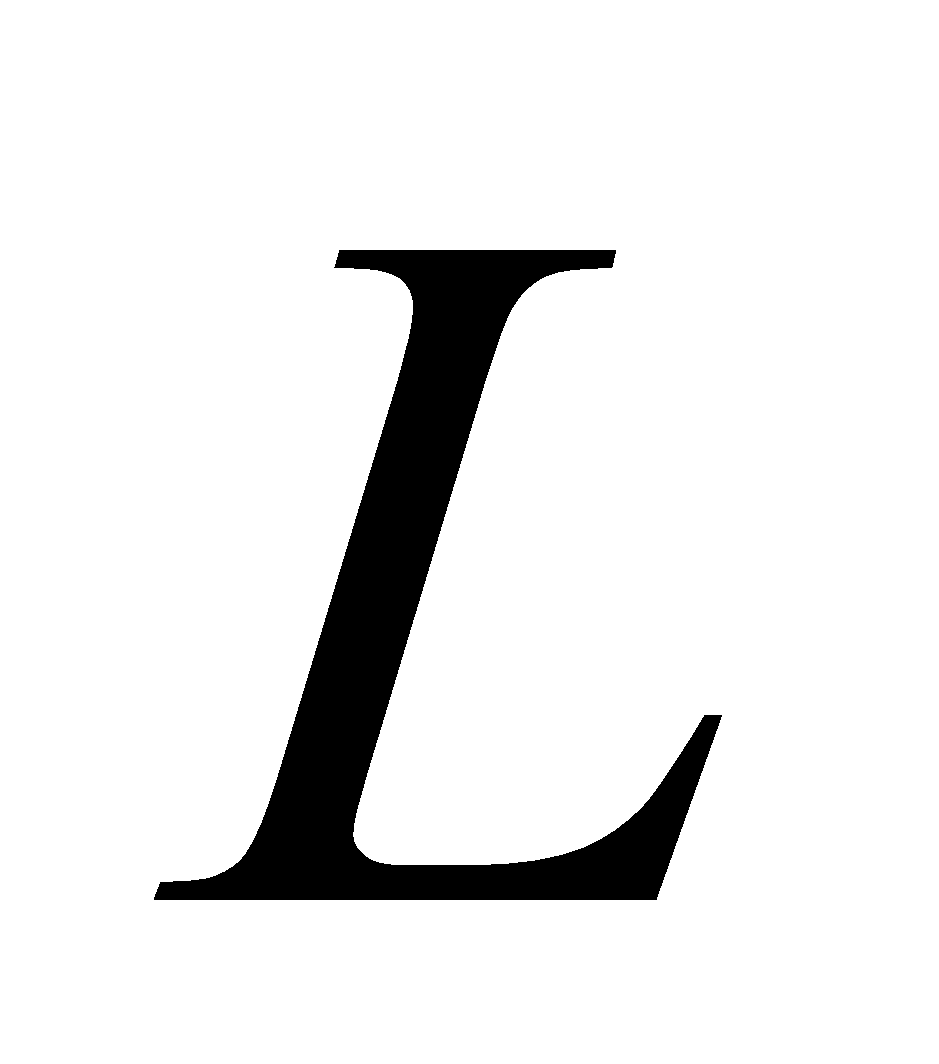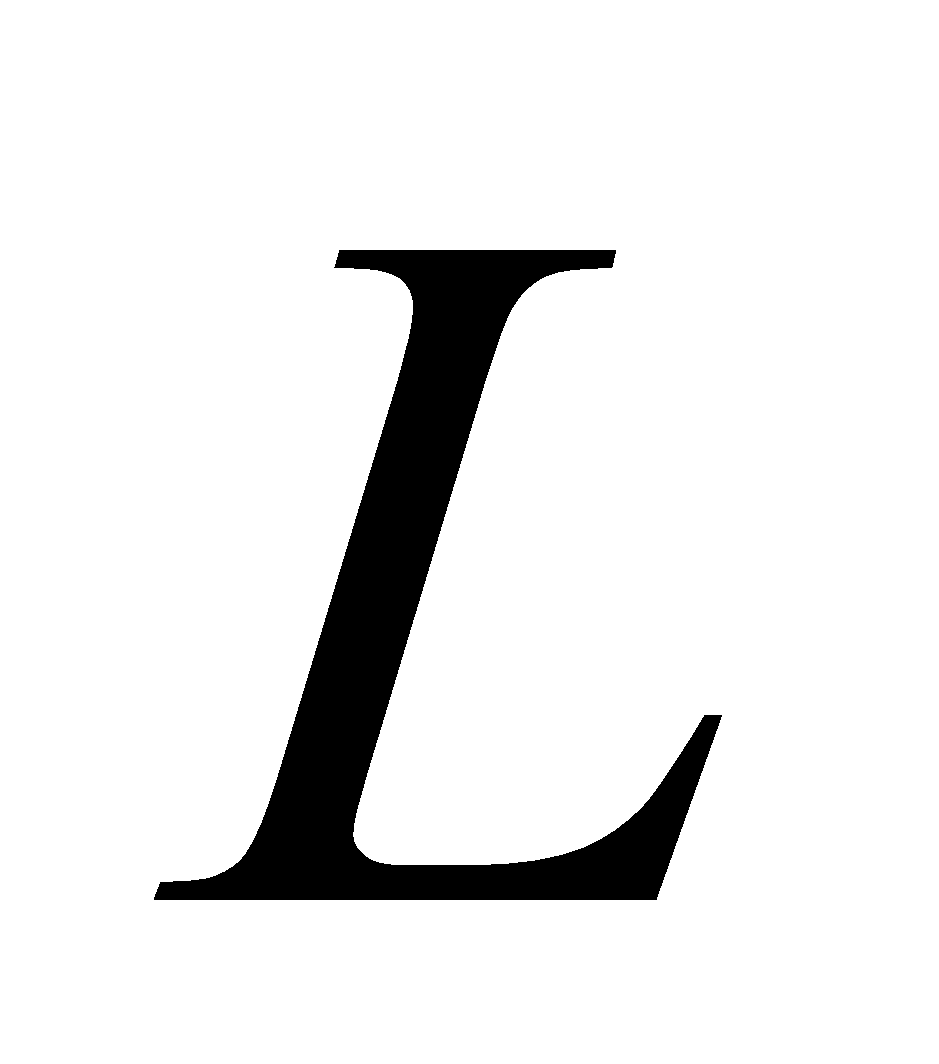Let be the set of all lines in the and be the relation in defined by

. Show that is an equivalence relation. Find the set of all lines related to the line. 3+1=4

3. If prove that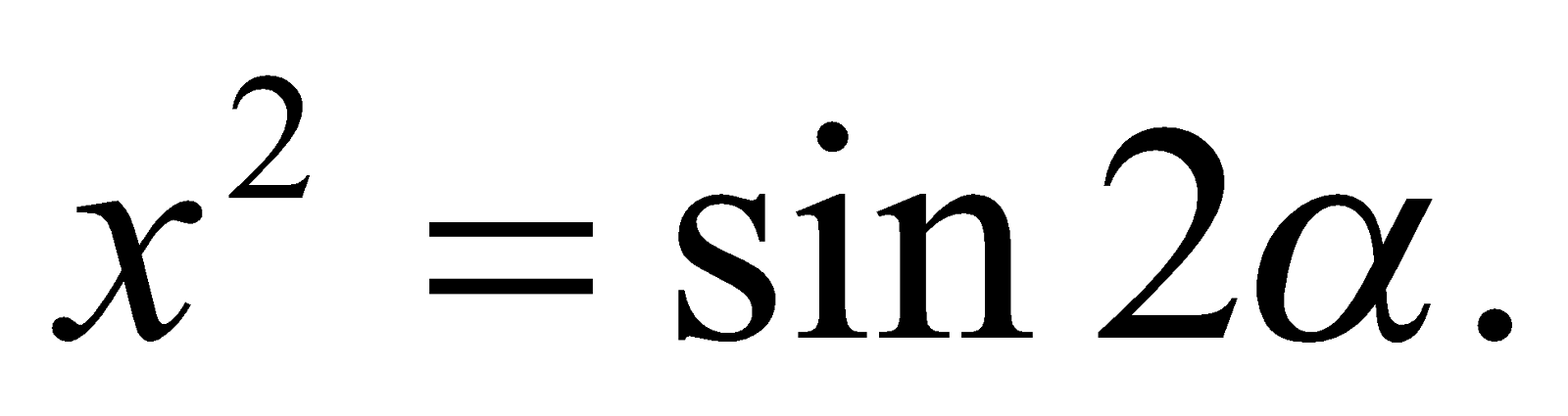

4. If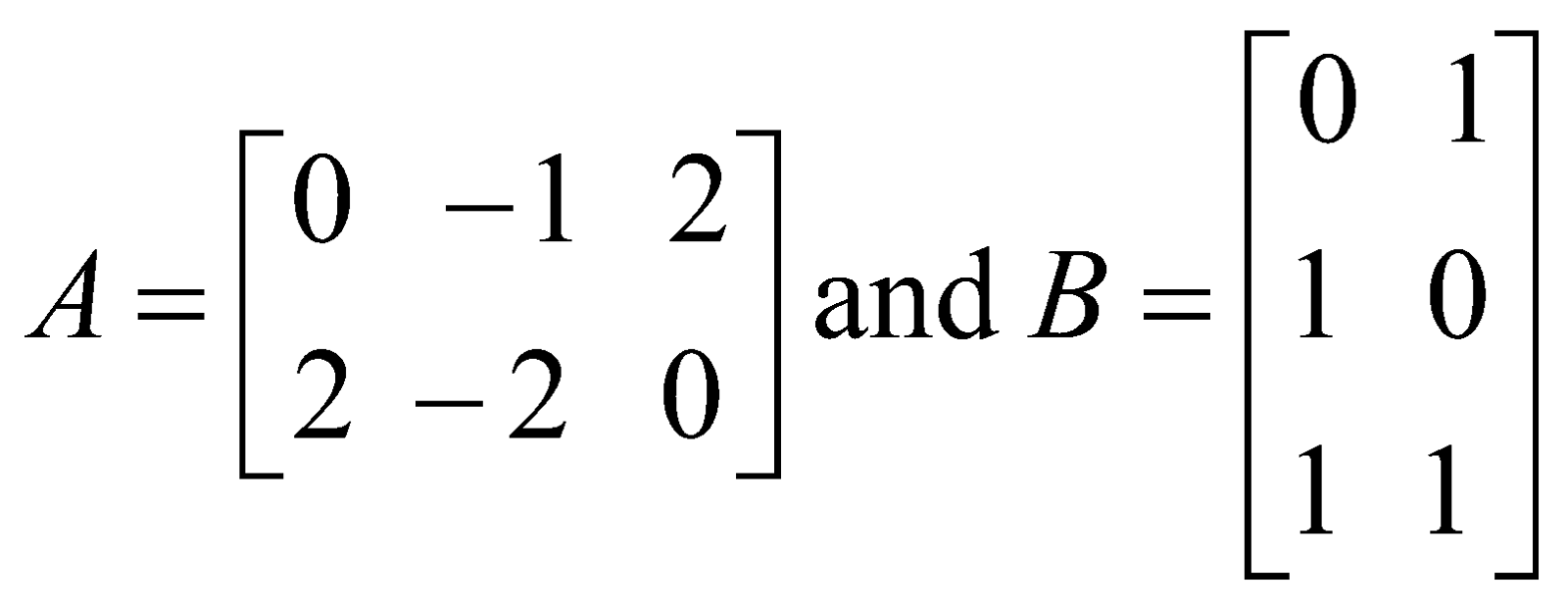, find a matrix such that, where 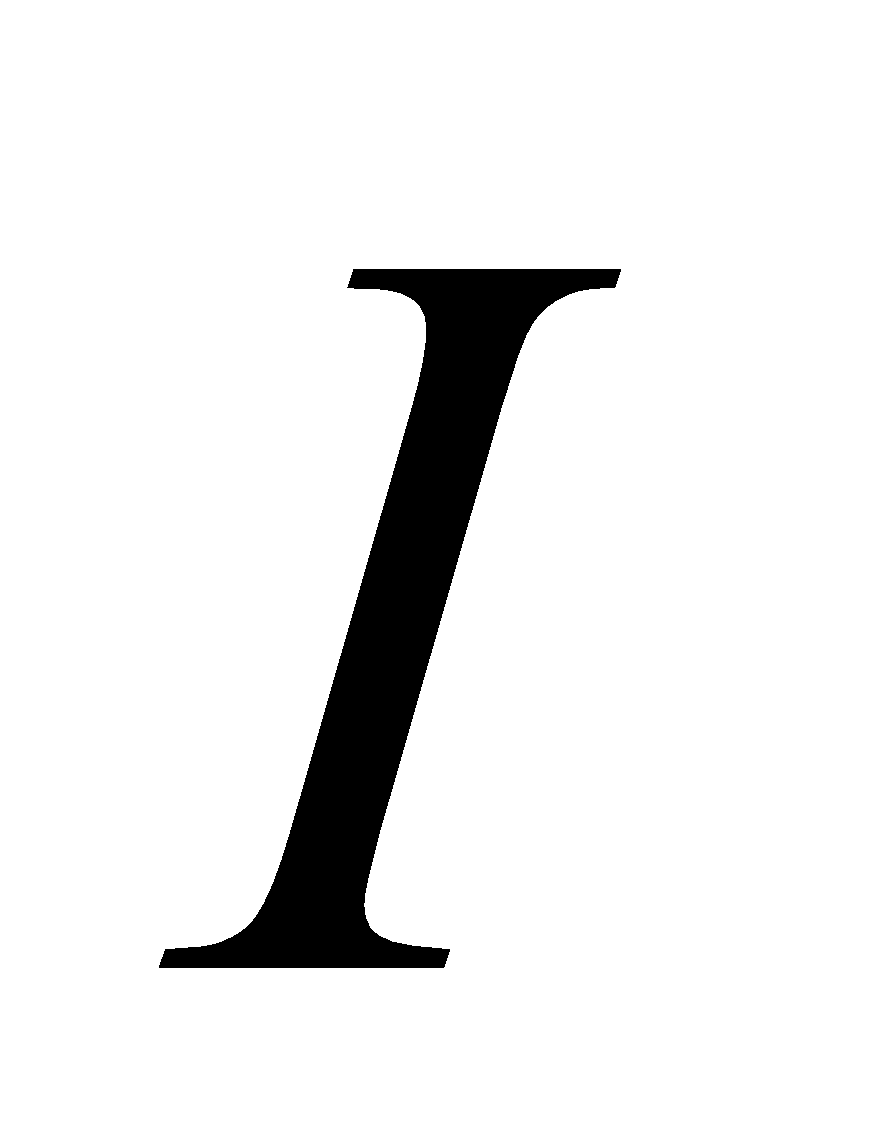is the unit matrix.   4

Or

Using elementary row operation, find the inverse of the matrix 4

5. If then find the values of for which is valid. 4

6. If a function is differentiable at a point, prove that it is continuous at that point. 4

Or

Using Rolle’s Theorem, find at what points on the curve in the tangent is parallel to.

7. Evaluate any one of the integrals: 4

1. 
2. 

8. Prove that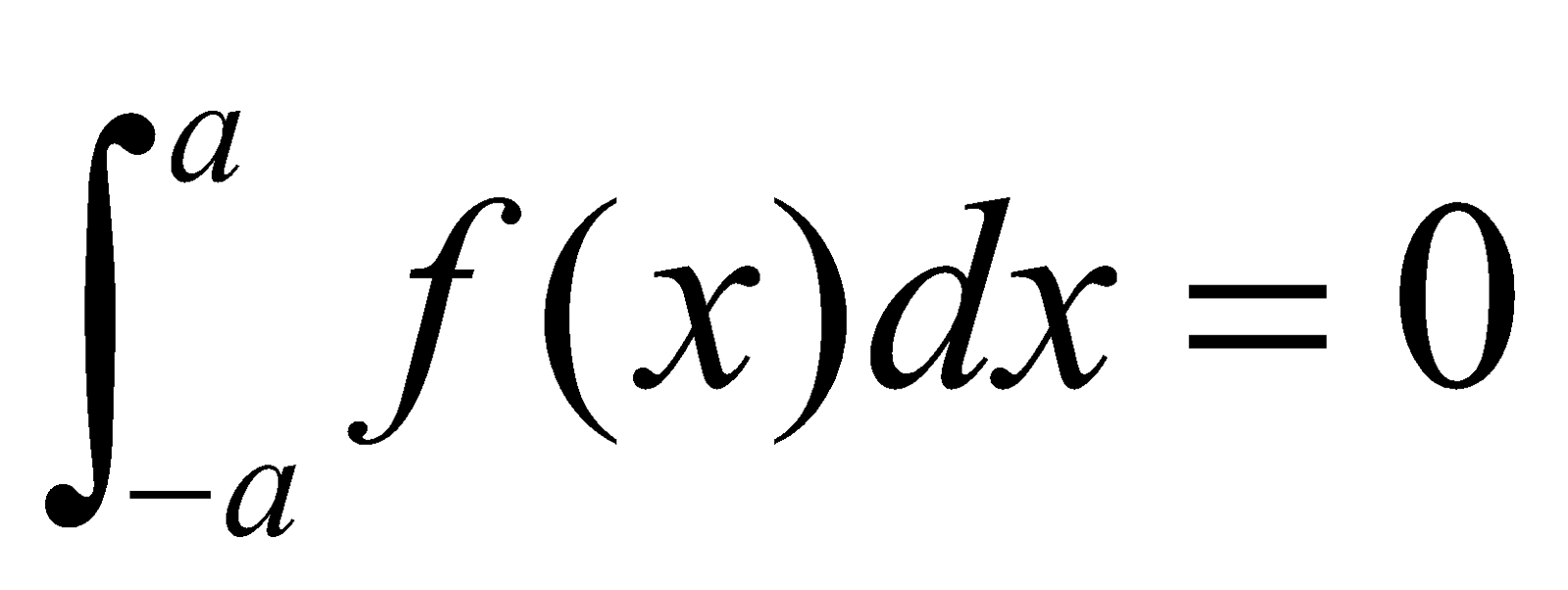, when is an odd function. Hence evaluate 4

9. Solve (any one): 4

1. 
2. 

10. Find the equation of a curve passing through the origin, given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the co-ordinates of the point. 4

11. Using vectors prove that angle in a semicircle is a right angle. 4

Or

Using vectors prove that 4

12. Find the vector equation of a plane in normal form. 4

Or

Find the equation of a plane passing through a given point and perpendicular to a given vector in vector form.

13. Assume that each child born is equally like to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls, given that 4

1. The youngest is a girl,
2. At least one is a girl?

Or

The probability of a shooter hitting a target is 3/4. How many minimum numbers of times must he/she fire so that the probability of hitting the target at least once is more than 0.99?

14. If x, y, z are all different and 6

Prove that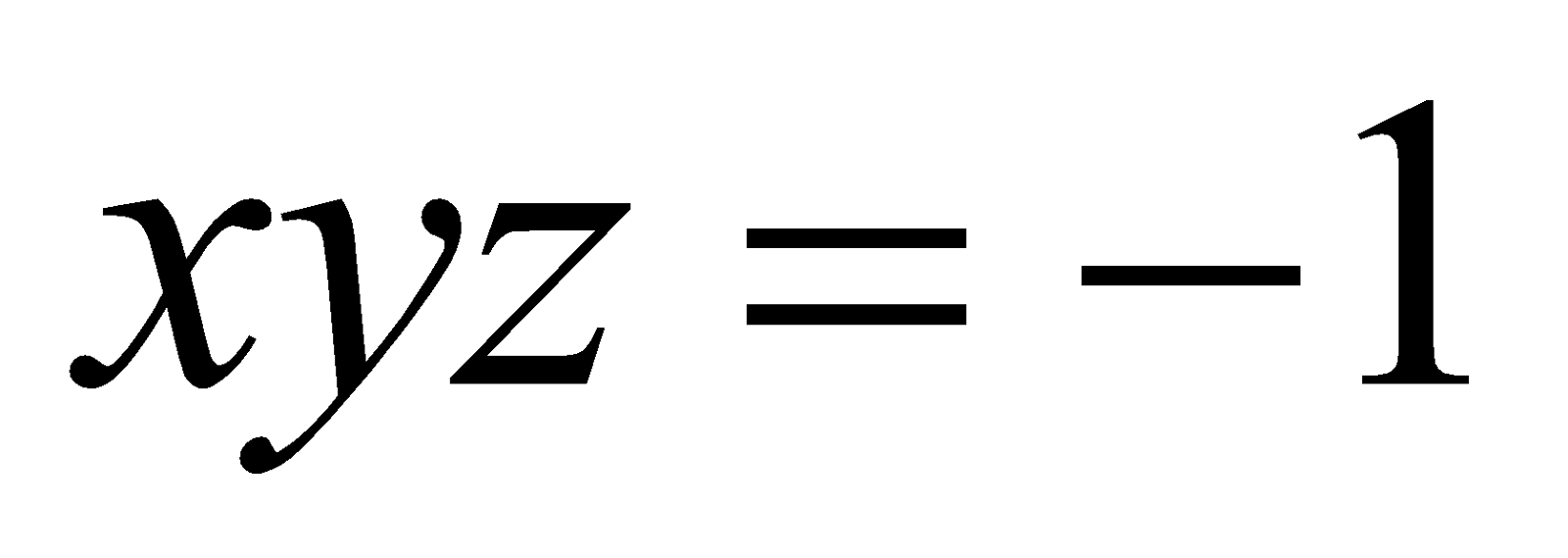

Or

If 6

Then find the value of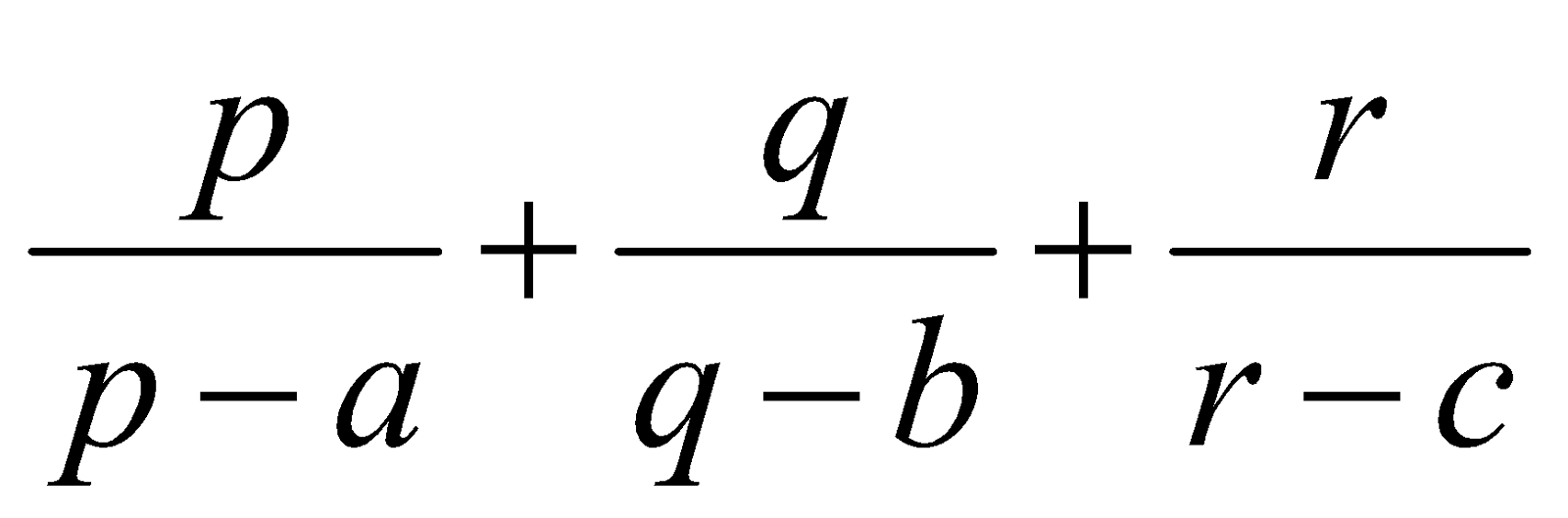

15. Find the maximum and minimum value of the following functions; if exist. 3+3=6

1. 
2. 

Or

Find the maximum area of an isosceles triangle inscribed in the ellipse with its vertex at one end of the major axis. 6

16. Evaluate: 6

Or

Evaluate 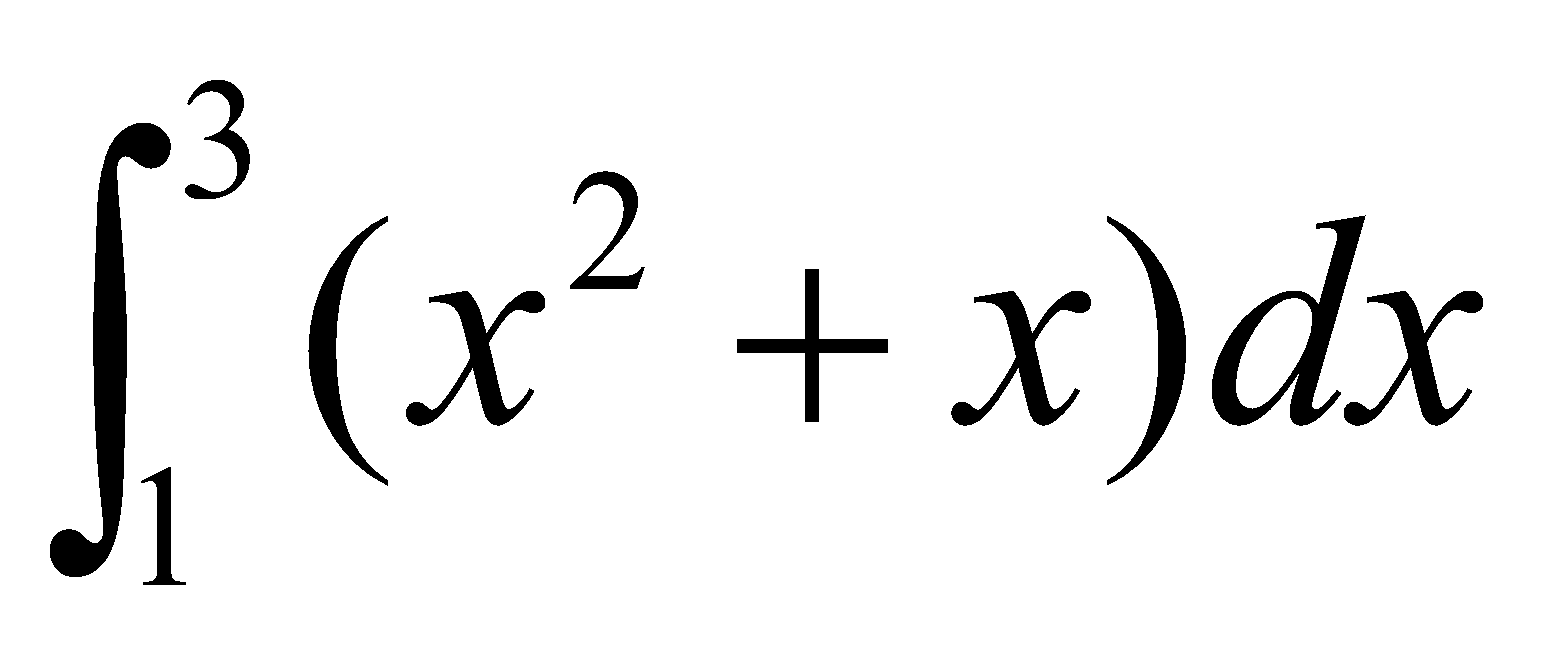as the limit of a sum.

17. Find the area bounded by

And 6

Or

Find the ratio in which the area bounded by the curves and 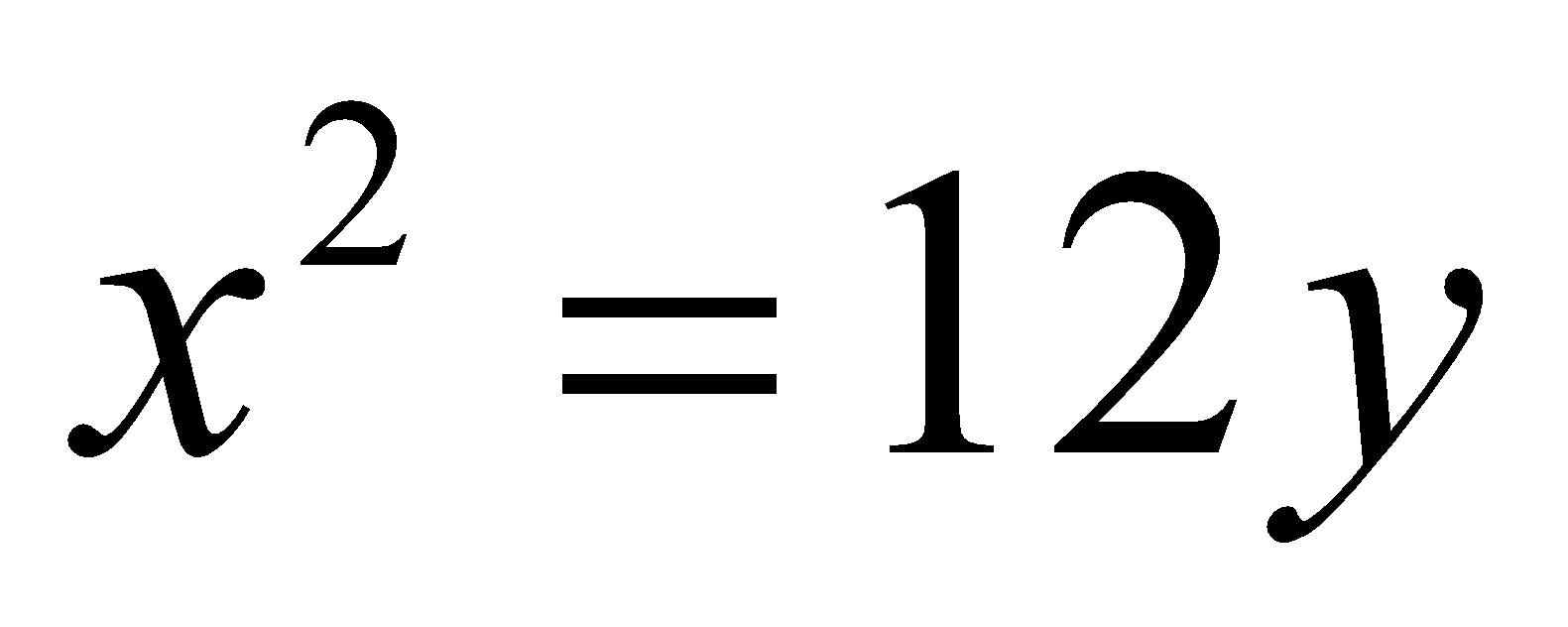is divided by the line.

18. Show that the lines

And are coplanar

And, find the equation of the plane containing both these lines. 6

19. A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making, while a cricket bat takes 3 hours of machine time and 1 hour of craftman’s time. In a day the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman’s time. If the profit on racket and on a bat is Rs. 20 and Rs. 10 respectively, find the maximum profit of the factory when it works at full capacity. 6