2014
MATHEMATICS
Full Marks: 100
Pass Marks: 30
Time: 3 hours
The figures in the margin indicate full marks for the questions
1. Answer the following questions: 1x10=10
- Is multiplication a binary operation on the set {0}
- If
write down the value of
.
- If A be a square matrix of order 2 whose determinant is
, find the value of
- What is the number of all possible
matrices with entries 0 or 1?
- If
be two matrices and
then what is the relation among
?
- What is the value of
if a function
is continuous at
and
?
- State whether it is true or false: “The derivative of an even function is always an even function”.
- If
and
are two mutually perpendicular unit vectors, what is the value of
- What is the general equation of a plane parallel to
- Let l, m, n be the direction cosines of the line
where
be any point on
where
. What is the co-ordinate of the mid-point of
2. Let 
be a non-empty set and 
be the power set of. Consider the binary operation * on 
defined by
. Show that is the identity element as well as the only invertible element in 
w.r.t * 4
be a non-empty set and be the power set of. Consider the binary operation * on defined by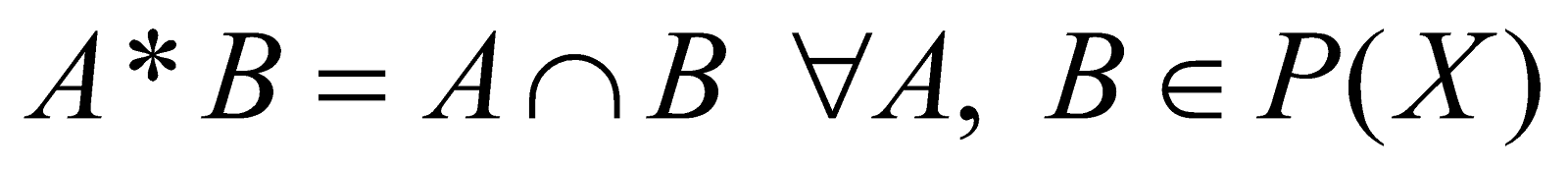. Show that is the identity element as well as the only invertible element in w.r.t * 4
3. Solve the following equation for
: 4
: 4
Or
4. Answer the following questions: 2+2=4
- If
and
are two matrices such that
then find the value of
.
- Show that the diagonal elements of a skew-symmetric matrix are all zero.
5. Prove that the function given by 
is not differentiable at
. Also examine the continuity at that point. 4
is not differentiable at. Also examine the continuity at that point. 4
Or
If 
show that 4
show that 4 
6. If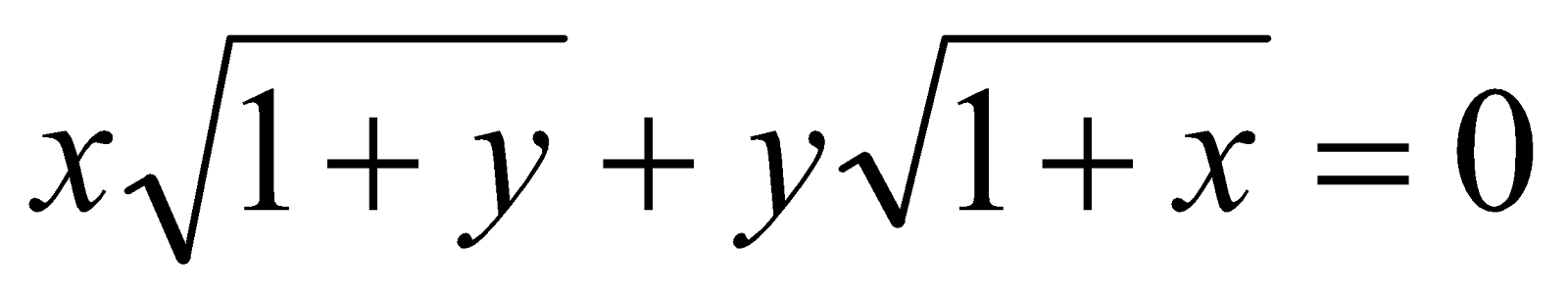 
then show that
. 4
then show that. 4
7. Integrate
8. Evaluate
Or
9. Answer any two of the following questions: 4x2=8
- Solve
- Find the particular solution of the differential equation
given that
when
.
- Find the solution curve passing through the point
of the differential equation
10. Show that, for any vector 
4
4
Or
Let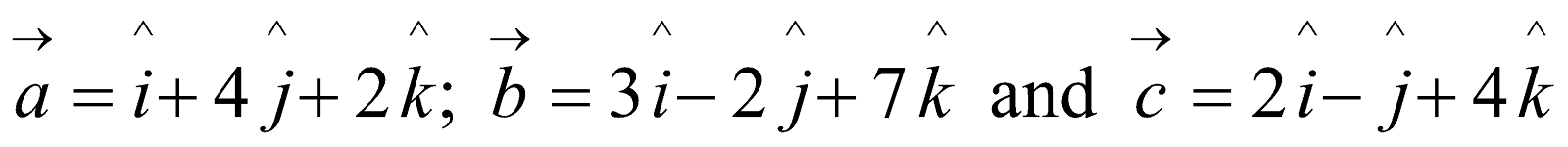
. Find the vector 
which is perpendicular to both
, 
and
. 4
. Find the vector which is perpendicular to both, 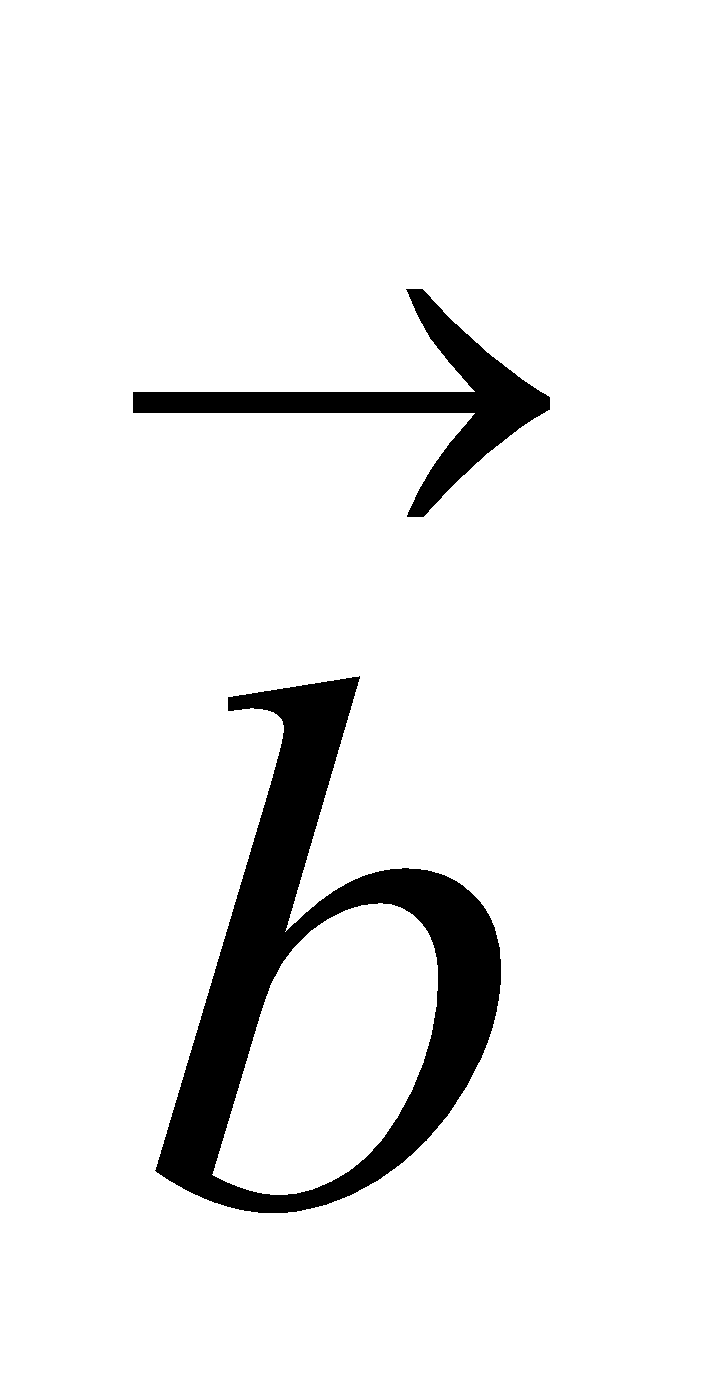and . 4
11. Find the co-ordinates of the foot of the perpendicular drawn from origin to the plane
. 4
. 4
12. Let 
denote the sum of the numbers obtained when two fair dice are rolled. Find the variance of 
. 4
denote the sum of the numbers obtained when two fair dice are rolled. Find the variance of . 4
Or
Two cards are drawn simultaneously (or successively without replacement) from a well shuffled pack of 52 cards. Find the mean and variance of the number of kings. 4
13. If a, b, c is real numbers and 6
Prove that either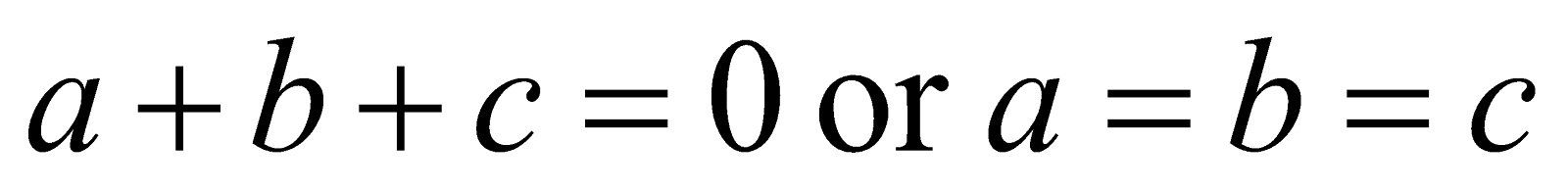 
Or
Without expanding at any stage prove that
14. Find the equation of tangents of the curve 
that are parallel to the line
. 6
that are parallel to the line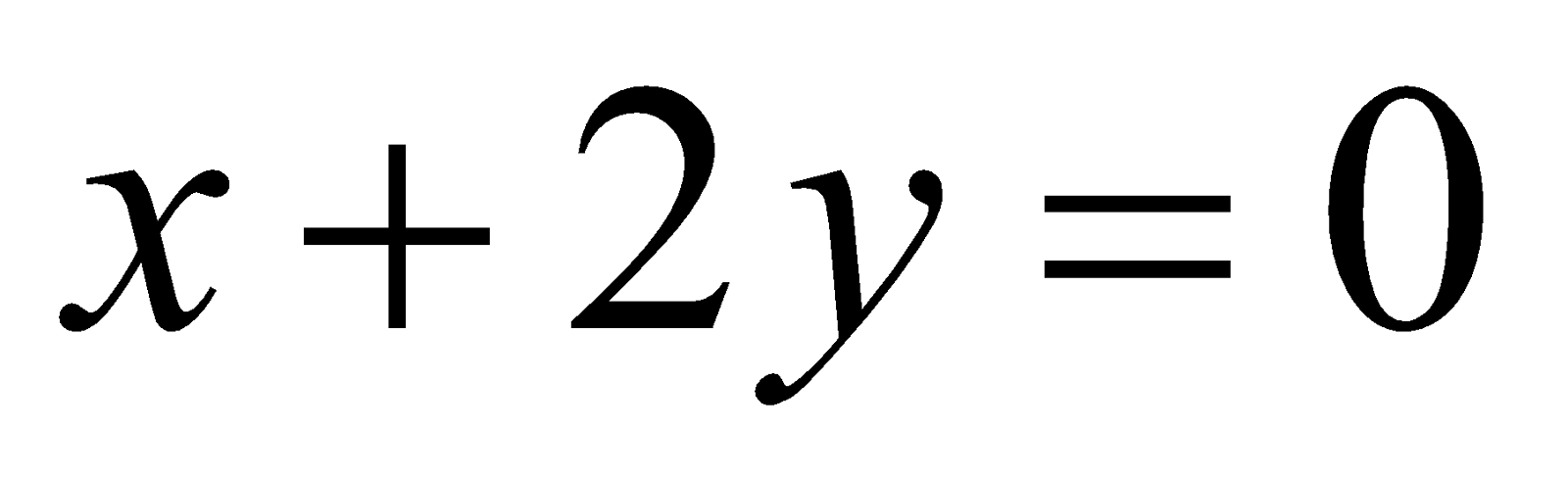. 6
Or
Show that 3+3=6
- The function
given by
Is always a strictly increasing function in 
. Has maximum at
.
15. Evaluate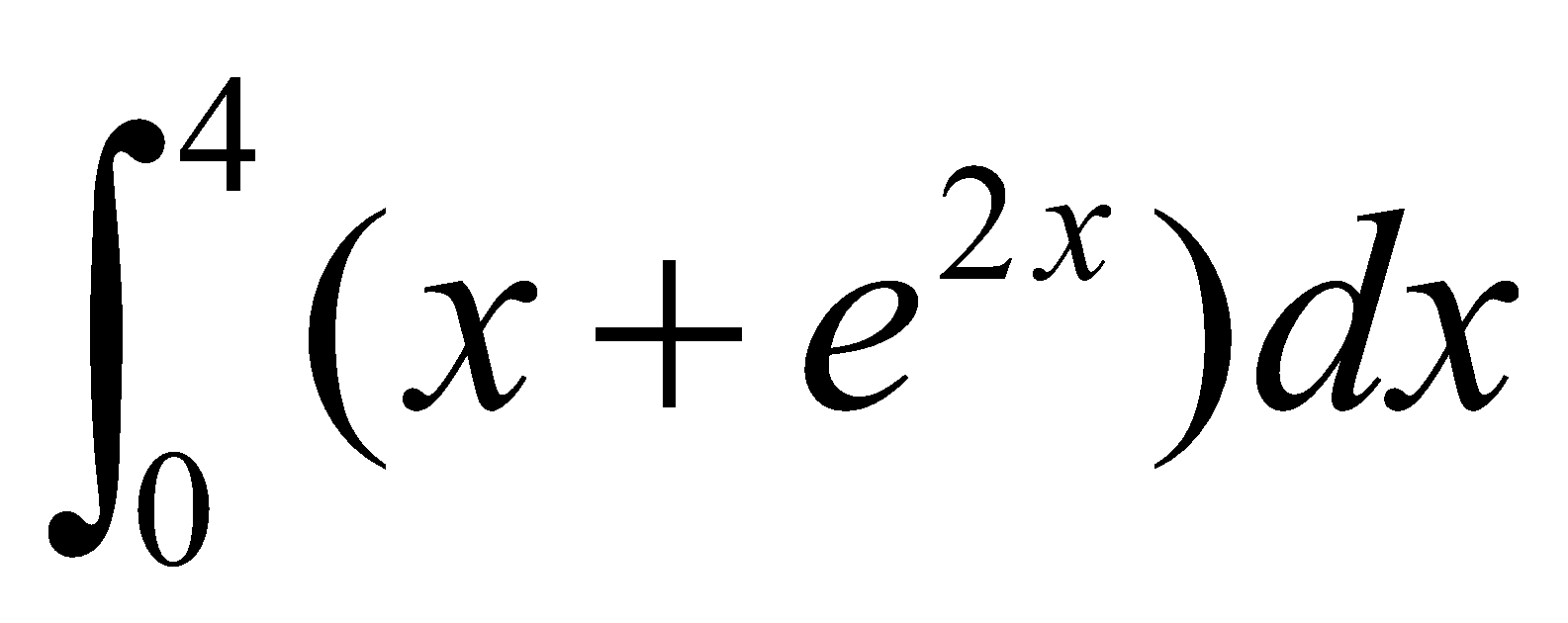 
by expressing it as the limit of a sum.
by expressing it as the limit of a sum.
16. Find the angle between the line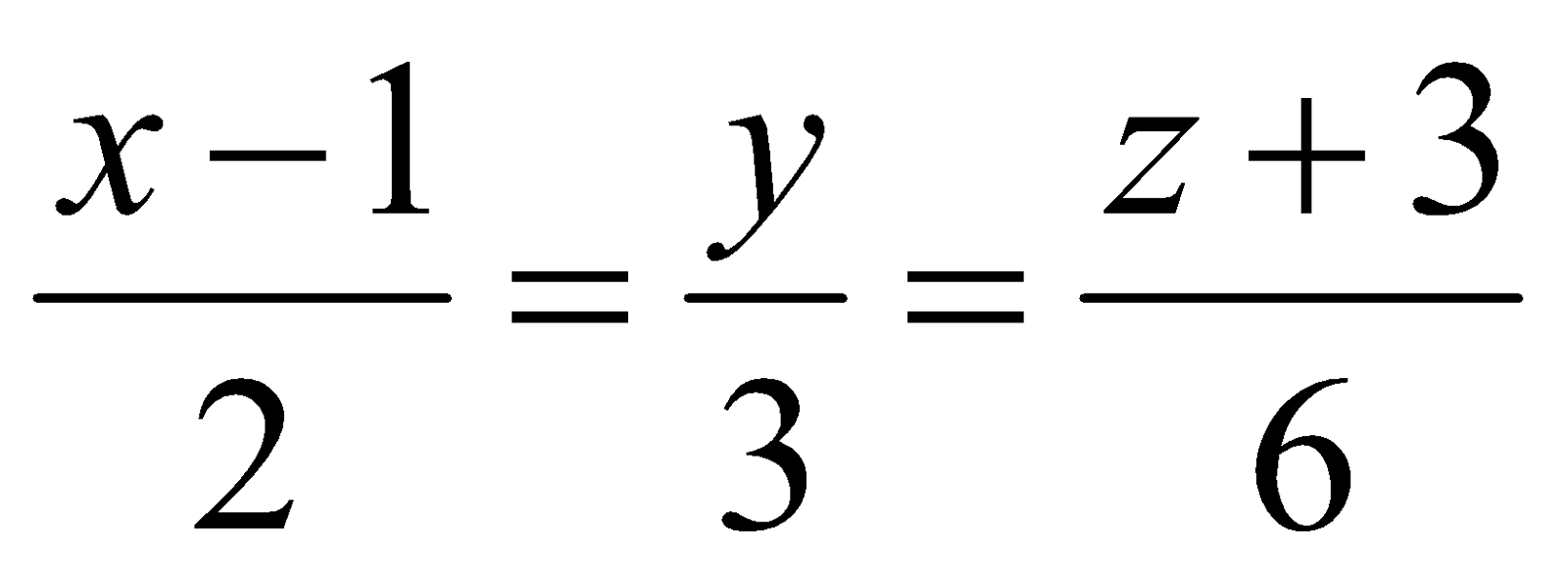 
and the plane
. Also find the point at which the line intersects the given plane. 6
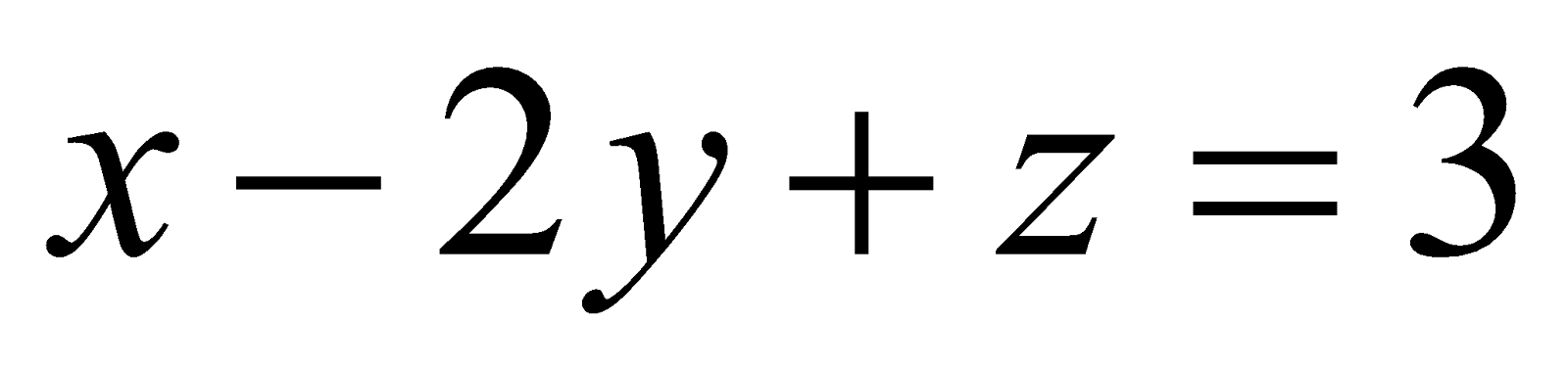and the plane. Also find the point at which the line intersects the given plane. 6
Or
Find the shortest distance and the equation of shortest distance between the lines
.
17. Find the area of the region in the 1st quadrant enclosed by the x-axis, the line 
and the circle 
6
and the circle 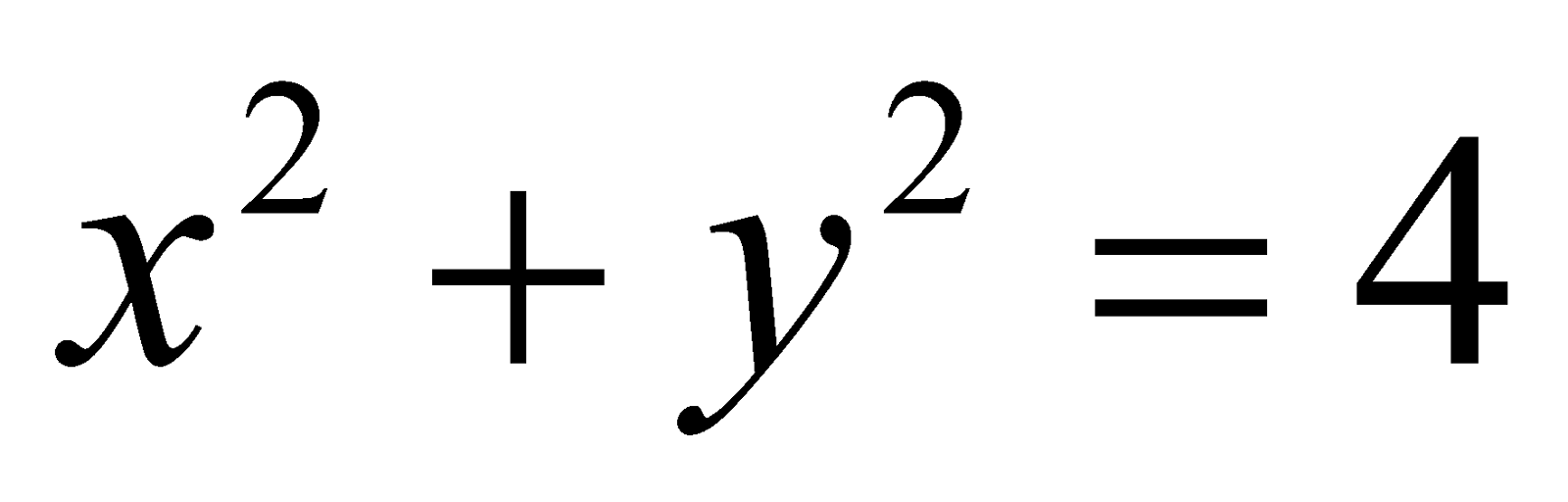6
Or
Find the area of the region bounded by the parabola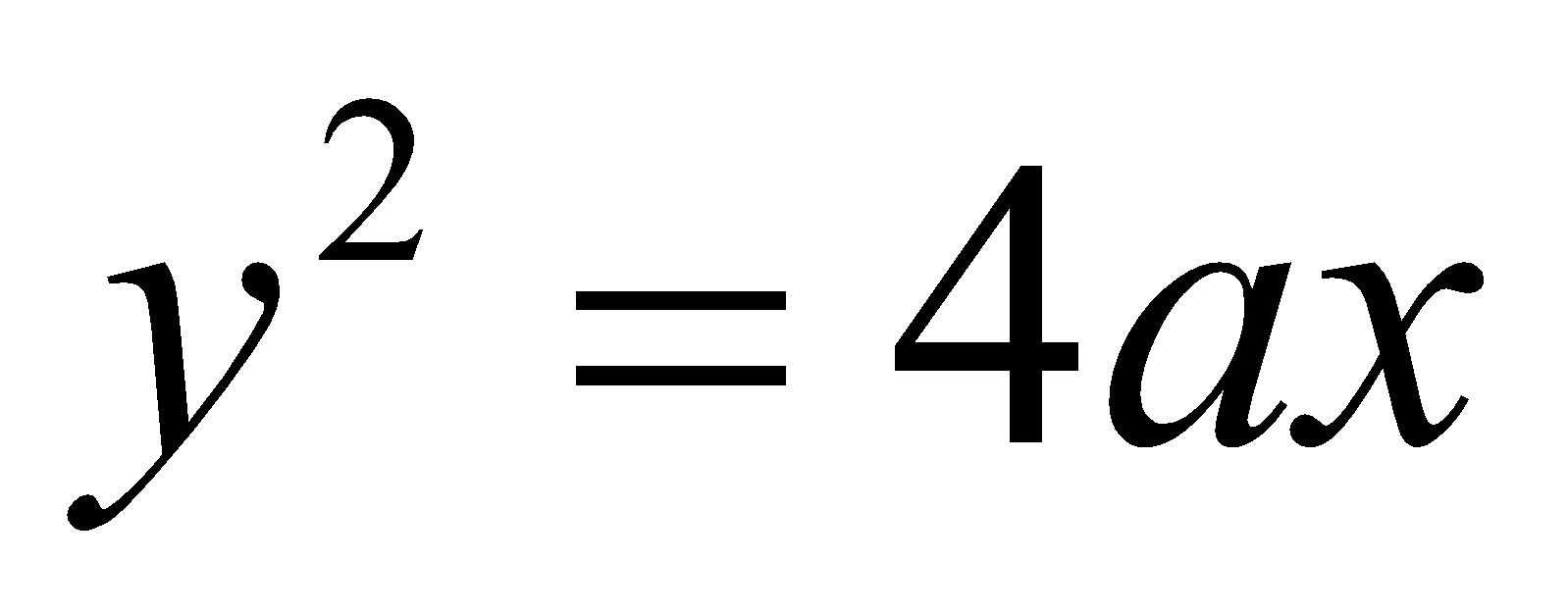 
and
. 6
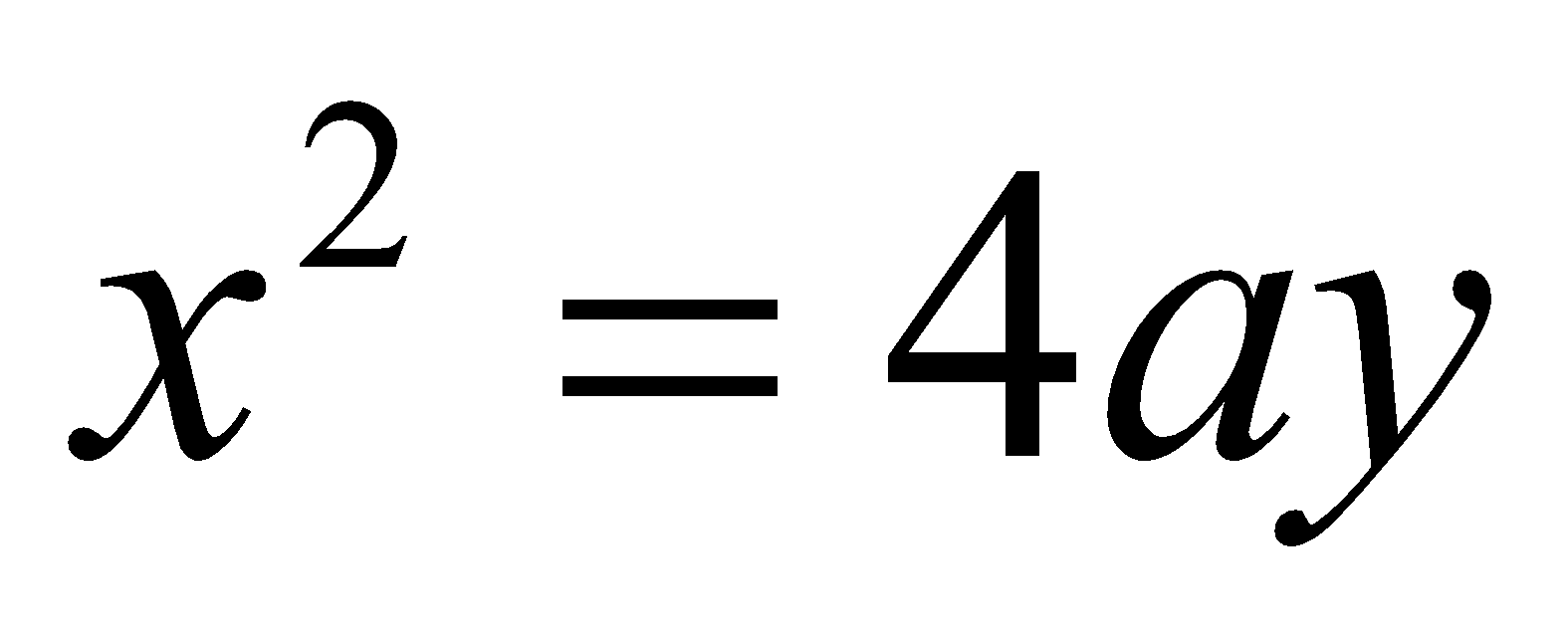and. 6
18. Showing the feasible region, solve graphically the following linear programming problem: 6
Maximize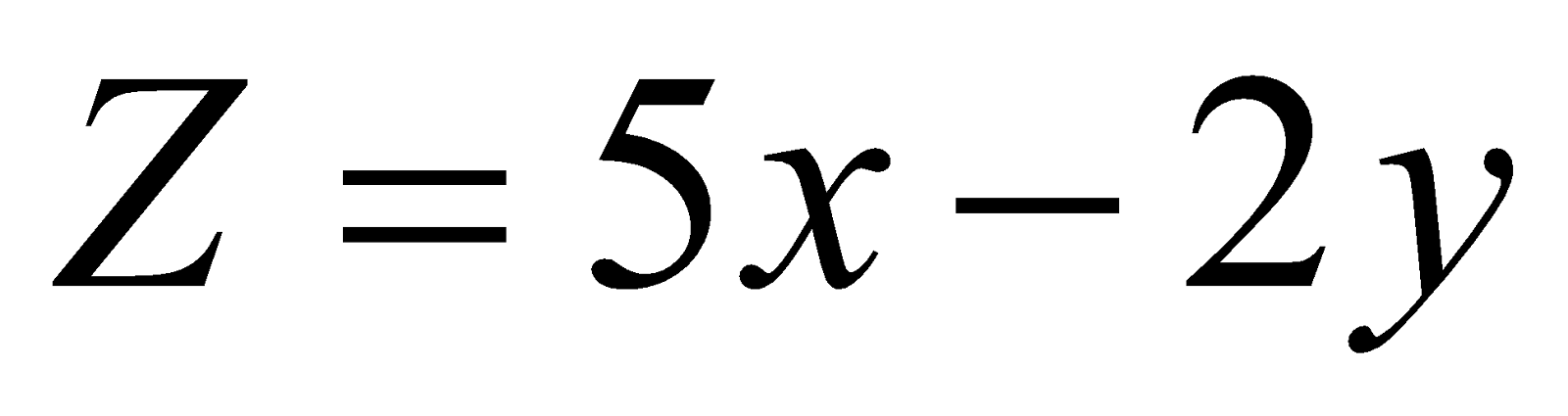 
Subject to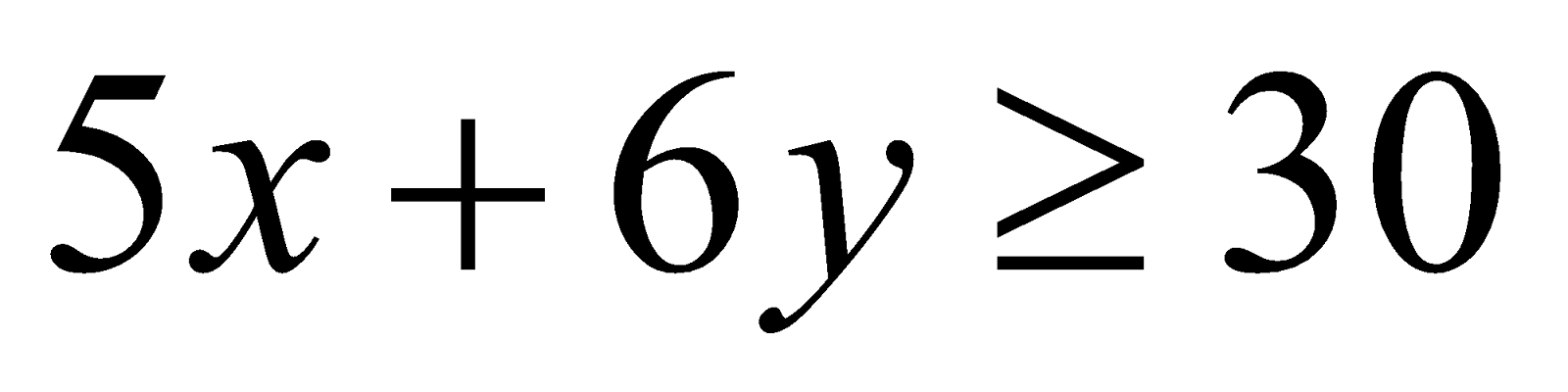 
19. There are three coins. One is a two headed coin (having heads on both sides), another is a biased coin that turns up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed. It shows head. What is the probability that it was the two headed coin? 6
Or
Probability of solving a specific problem independently by A and B are 1/2 and 1/3 respectively. If both try to solve the problem independently, find the probability that
- The problem is solved.
- Exactly one of them solves the problem. 3+3=6