[BA 4th Sem Question Papers, Dibrugarh University, 2017, Mathematics, General, A: (Linear Programming]
1. (a) Define hypersphere. 1
(b) Write the mathematical form of a general linear programming problem. 2
(c) Answer any one question: 4
- Prove that the intersection of two convex sets is again a convex set.
- What are the limitations of LP model?
(d) Answer any one question: 5
- Solve graphically the following LPP:
Maximize
Subject to
And 
- Solve graphically the following LPP:
Minimize
Subject to
And 
2. (a) What do you mean by ‘feasible solution’ of linear programming problem? 1
(b) Define slack and surplus variable of a linear programming problem. 2
(c) Answer any one question: 7
- Using the simplex methods, solve the linear programming problem.
Maximize
Subject to
And 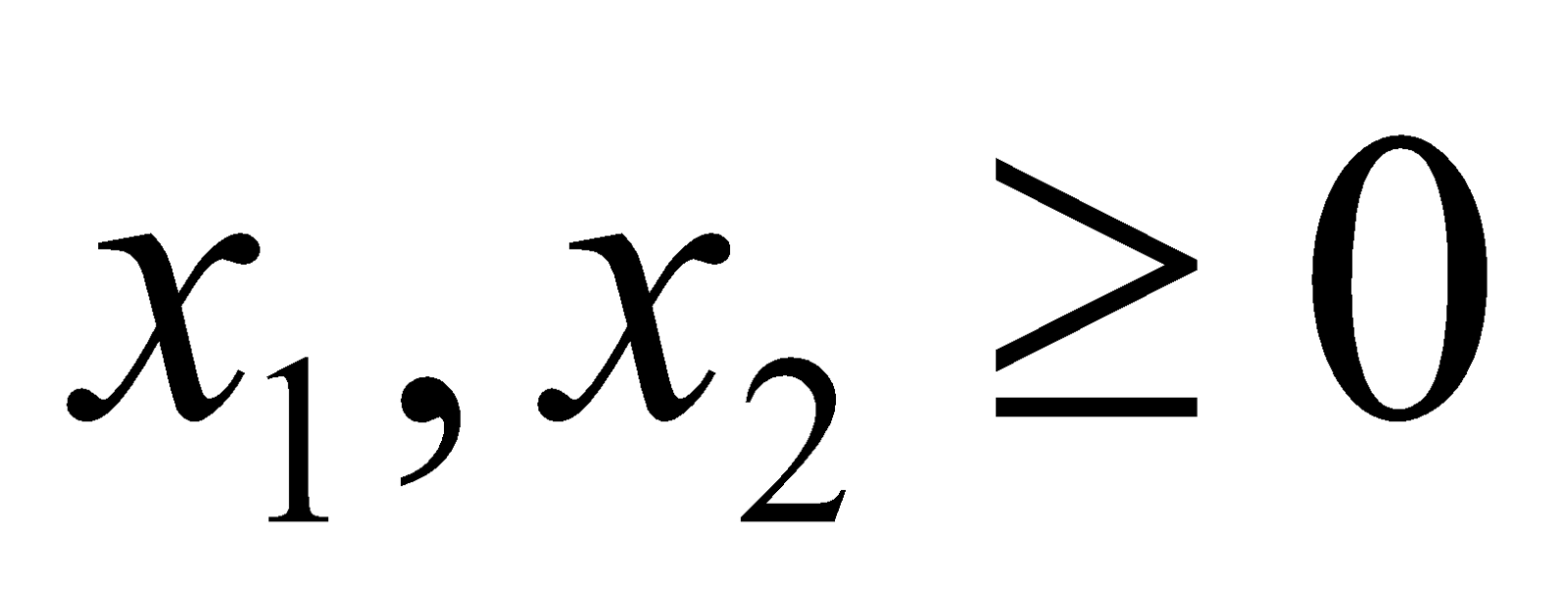
- Discuss the computational procedure of simplex method to solve a linear programming problem.
(d) Answer either (i) or (ii): 8
- Solve the following LPP using two-phase method:
Maximize
Subject to
And 
- Using Big-M method, solve the following LPP:
Minimize
Subject to
And 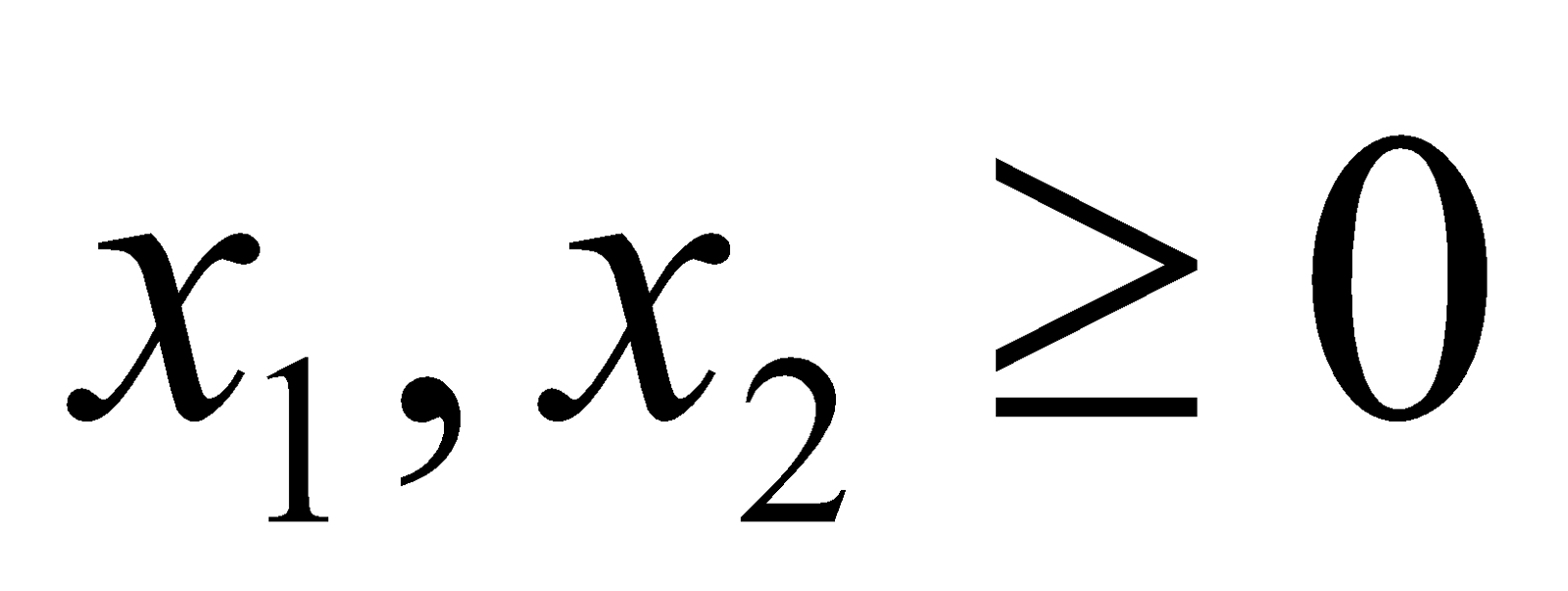
3. (a) Write True or False: 1
The dual of a maximization problem is a minimization problem.
(b) Write the dual of the following LPP: 2
Maximize
Subject to
And 
(c) Answer any one question: 5
- Obtain the dual problem of the following primal LP problem:
Minimize
Subject to
And 
- Prove that dual of the dual of a given primal problem is the primal itself.
4. (a) Answer the following questions: 1x2=2
- Define unbalanced transportation problem.
- Define feasible solution of transportation problem.
- Write the mathematical formulation of a transportation problem.
Also Read: Dibrugarh University Question Papers
5. Answer any one question: 8
- Obtain an optimal solution using Vogel’s method of the following transportation problem:
D1
|
D2
|
D3
|
D4
|
Supply
| |
S1
|
19
|
30
|
50
|
10
|
7
|
S2
|
70
|
30
|
40
|
60
|
9
|
S3
|
40
|
8
|
70
|
20
|
18
|
Demand
|
5
|
8
|
7
|
14
|
34
|
- Write short notes on:
- North-West corner rule.
- Least cost method.
***

