[BA 4th Sem Question Papers, Dibrugarh University, 2014, Mathematics, General, A: Linear Programming]
(GROUP – A)
1. (a) Define hypersphere. 1
(b) What are four basic assumptions necessary for linear programming model? 2
(c) Answer any one question: 4
- What are the limitations of LP model?
- Prove that hyperplane is a convex set.
(d) Answer any one question: 5
- Solve graphically the following LPP:
Maximize
Subject to
And 
- Solve graphically the following LPP:
Minimize
Subject to
And 
2. (a) What do you mean by ‘decision variable’ in linear programming problem? 1
(b) Mention the difference between ‘feasible solution’ and ‘basic feasible solution’ in a linear programming problem. 2
(c) Using simplex method, solve any one of the following LPP: 7
- Maximize
Subject to
And 
- Minimize
Subject to
And 
(d) Answer either (i) or (ii): 8
- Solve LPP using two-phase method:
Maximize
Subject to
And 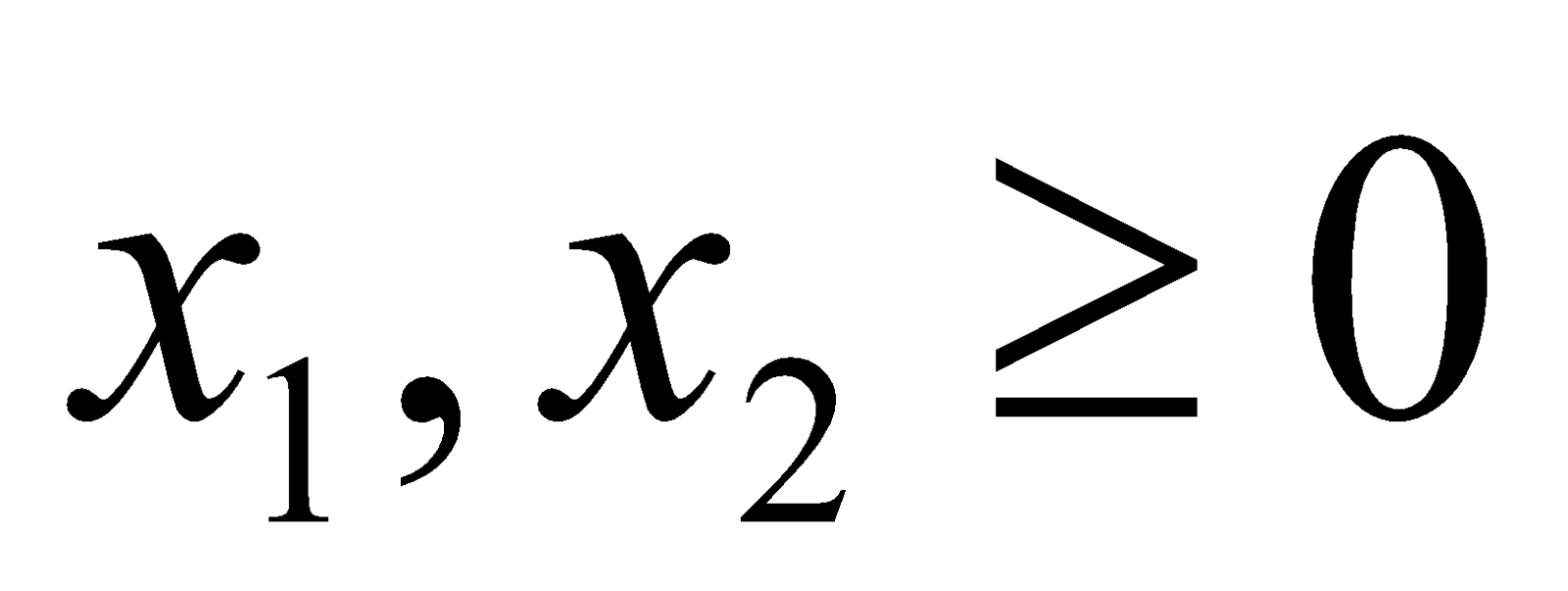
- Using Big-M method, solve the following LPP:
Maximize
Subject to
And 
3. (a) What is ‘dual’ linear programming problem? 1
(b) Write the dual of the following LPP: 2
Maximize
Subject to
And 
(c) Answer any one question: 5
- Find the dual of the primal:
Maximize
Subject to
And 
- If
be any feasible solution to the primal max
, subject to
and
be any feasible solution to its dual, min
subject to
then show that
.
4. (a) Answer the following questions: 1x2=2
- Define ‘loop’ in a transportation problem.
- How many decision variables will be there in transportation problem containing m-sources and n-destinations?
(b) Write the mathematical formulation of a transportation problem. 2
Also Read: Dibrugarh University Question Papers
5. Answer any one question: 8
(a) Determine an initial basic feasible solution using northwest-corner method and least cost method, and compare their corresponding costs:
Supply
| |||||
4
|
6
|
9
|
5
|
16
| |
2
|
6
|
4
|
1
|
12
| |
5
|
7
|
2
|
9
|
15
| |
Demand
|
12
|
14
|
9
|
8
|
43
|
(b) Write short notes on Vogel’s approximation method.
(c) Prove that, in a balanced transportation problem having -origin and
-origin and -destinations
-destinations the exact number of basic variables is
the exact number of basic variables is .
.
***


Post a Comment
Kindly give your valuable feedback to improve this website.