2015
(May)
MATHEMATICS
(Major)
Course: 604
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions.
[ (a) Financial Mathematics
(b) Operations Research. ]
(a) Financial Mathematics
(Marks: 45)
1. (a) Describe briefly what you mean by market equilibrium. 2
(b) The supply set 
consists of the points 
such that 
and the demand set 
consists of the pointssuch that
. An excise tax of Rs. 2 per unit is imposed. Determine the new equilibrium price and quantity. 3
consists of the points such that and the demand set consists of the pointssuch that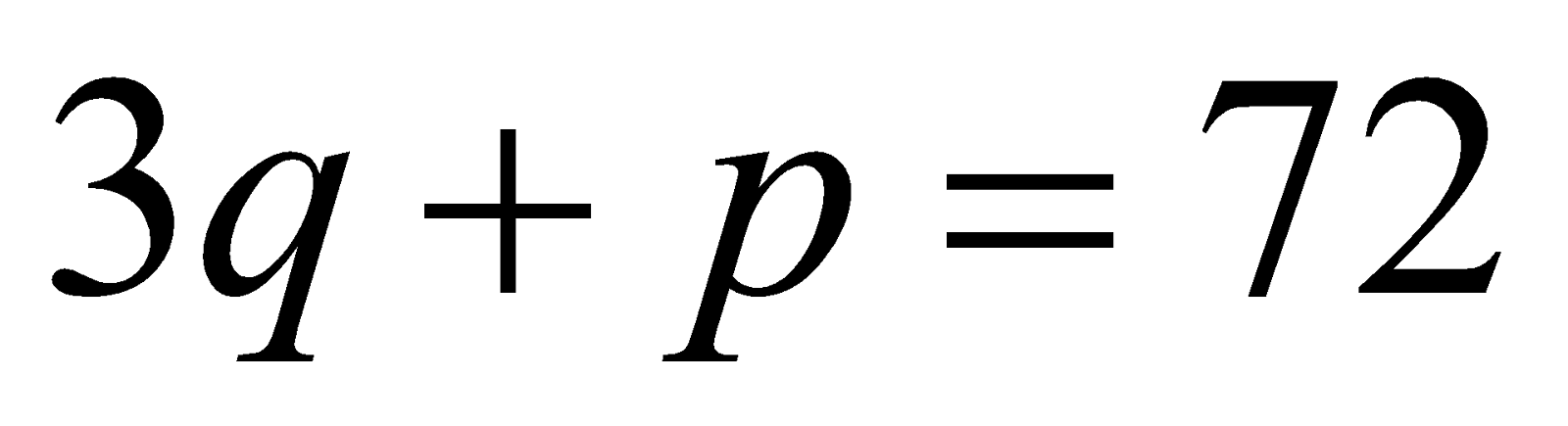. An excise tax of Rs. 2 per unit is imposed. Determine the new equilibrium price and quantity. 3
2. Describe the economic interpretation of cobweb model. 5
Or
The supply and demand sets are given by 
and
. Find the price sequence.
and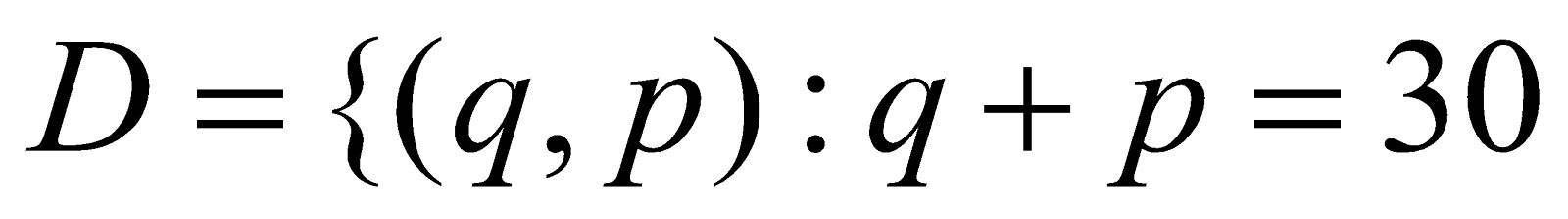. Find the price sequence.
3. Write a note on profit maximization. 5
Or
State briefly about optimization in an interval.
4. (a) Define elasticity of demand. 3
(b) For an efficient small farm, define start-up point and show that at start-up point, marginal cost is equal to average variable cost. 3
(c) For an efficient small farm, define break-even point. Show that at break-even point the derivative of average cost is zero. 4
5. (a) State True or False: Every critical point is a maximum. 1
(b) Find and classify the critical points of 
4
4
(c) Find the maximum values of 
5
5
6. (a) Define a technology matrix. 2
(b) Explain a two-industry economy with an example. 4
(c) The matrix for an investor is 
4
4
Show that the portfolio 
is riskless.
is riskless.
What return is the investor guaranteed?
(b) Operations Research
(Marks: 35)
7. State briefly about operations research techniques. 5
Or
Write a note on scopes and limitations of operations research.
8. (a) Prove that in an assignment problem if we add or subtract a constant to every element of a row (or column) in the cost matrix, then an assignment which minimizes the total cost on one matrix, also minimizes the total cost on the other matrix. 3
(b) Find the optimal assignment and the corresponding assignment cost from the following cost matrix: 7
A B C D E
1
2
3
4
5
|
9 8 7 6 4
5 7 5 6 8
8 7 6 3 5
8 5 4 9 3
6 7 6 8 5
|
Or
Find the optimal assignment profit from the following profit matrix:
I II III IV
A
B
C
D
|
42 35 28 21
30 25 20 15
30 25 20 15
24 20 16 12
|
9. (a) Who developed the dynamic programming technique? 1
(b) State what you mean by principle of optimality. 2
(c) Using dynamic programming, solve the following
: 7
: 7
Maximize
Subject to
Or
Maximize 
Subject to
10. (a) State whether the following statement is True or False: 1
Integer programming is a special class of linear programming problem in which decision variables have integer solution.
(b) Solve the followingby Gomory technique: 9
by Gomory technique: 9
Maximize 
Subject to
Or
Maximize 
Subject to
GROUP – B
[ (A) Space Dynamics
(b) Relativity]
(a) Space Dynamics
(Marks: 40)
1. Answer as directed: 1x3=3
- Choose the correct answer:
If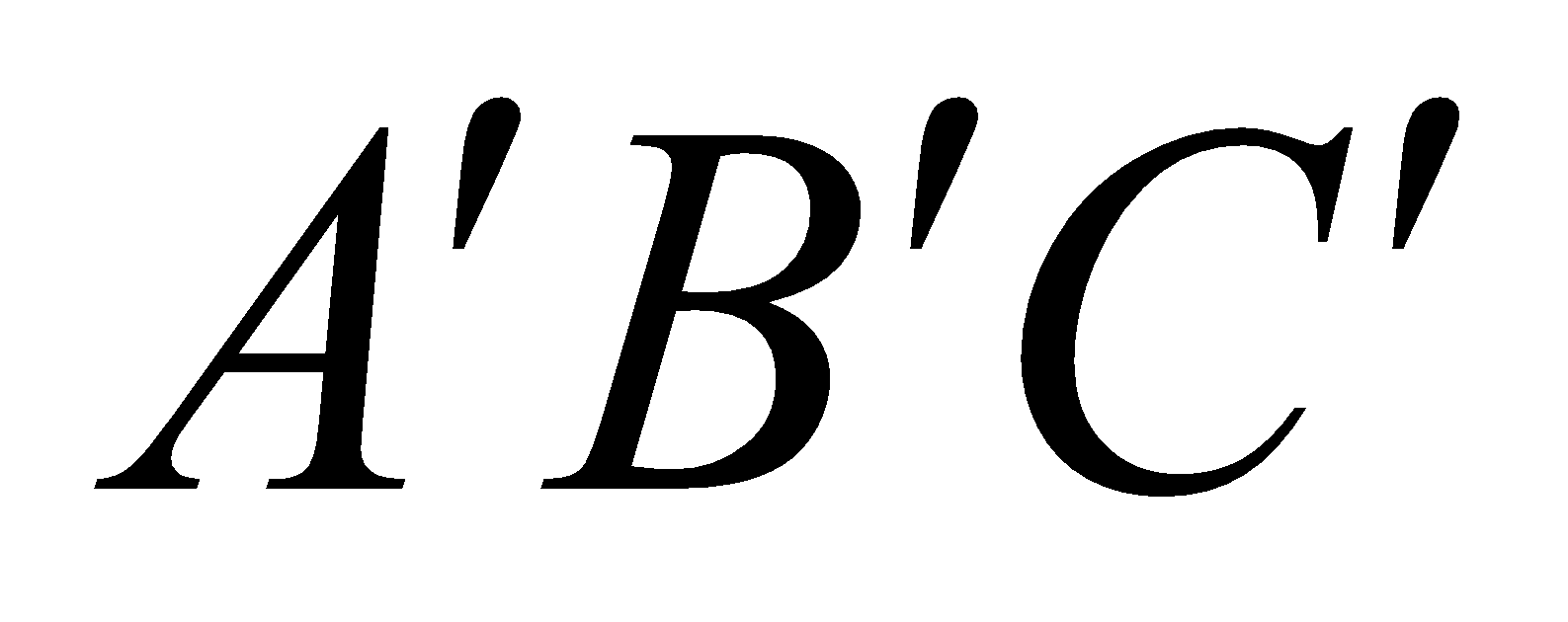 
is the polar triangle of the triangle
, then
is the polar triangle of the triangle, then
- State True or False:
A general spherical triangle has more then one right angle.
- Fill up the Gap:
In spherical triangle,
the circular parts are ____.
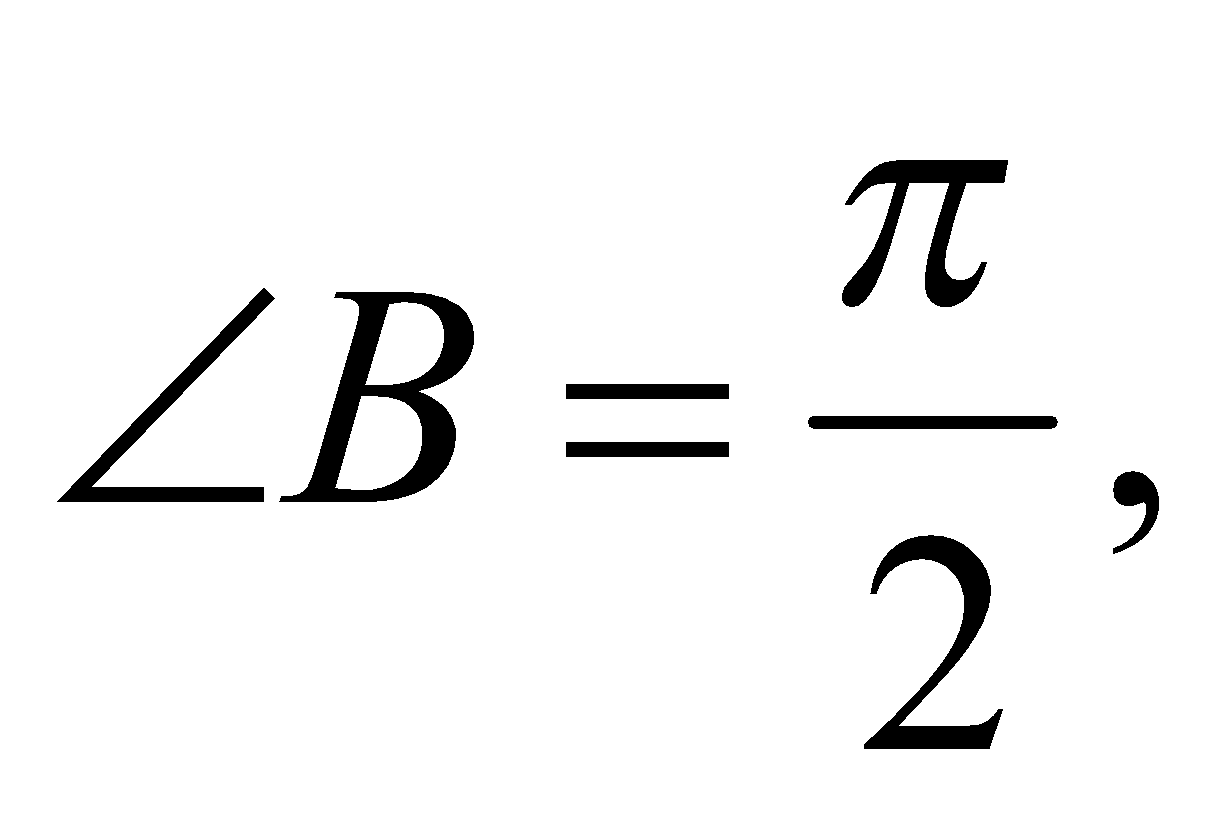,the circular parts are ____.
2. If one triangle is the polar triangle of another triangle, then prove that the later is the polar of the former. 2
3. State and prove the cosine formula of a spherical triangle. 5
Or
In any spherical triangle, prove that 
, prove that
4. In an equilateral spherical triangle, prove that 
3
, prove that 3
Or
In a spherical triangle,
and
is the middle point of 
, then show that
,andis the middle point of 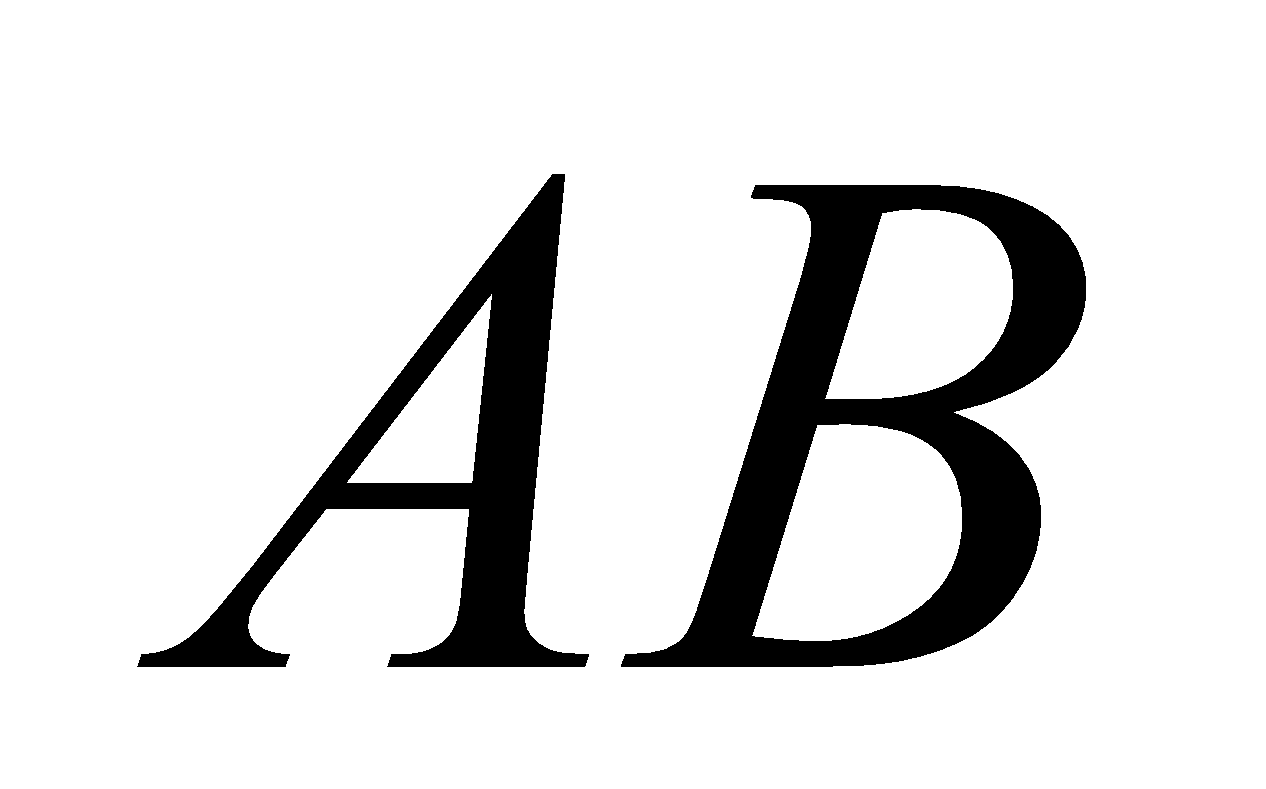, then show that 
5. If 
and
are respectively the equatorial system and ecliptic system of coordinates of a star, then prove that 
and 
where 
is the obliquity of the ecliptic. 3+3=6
andare respectively the equatorial system and ecliptic system of coordinates of a star, then prove that and where is the obliquity of the ecliptic. 3+3=6
6. Define the following: 2x2=4
- Annual motion of the sun.
- Rising and setting of stars.
7. Write short notes on the following (any two): 2x2=4
- Diurnal motion of heavenly bodies.
- Hour angle and parallactic angle of a star.
- Cardinal points and equinotical points.
8. If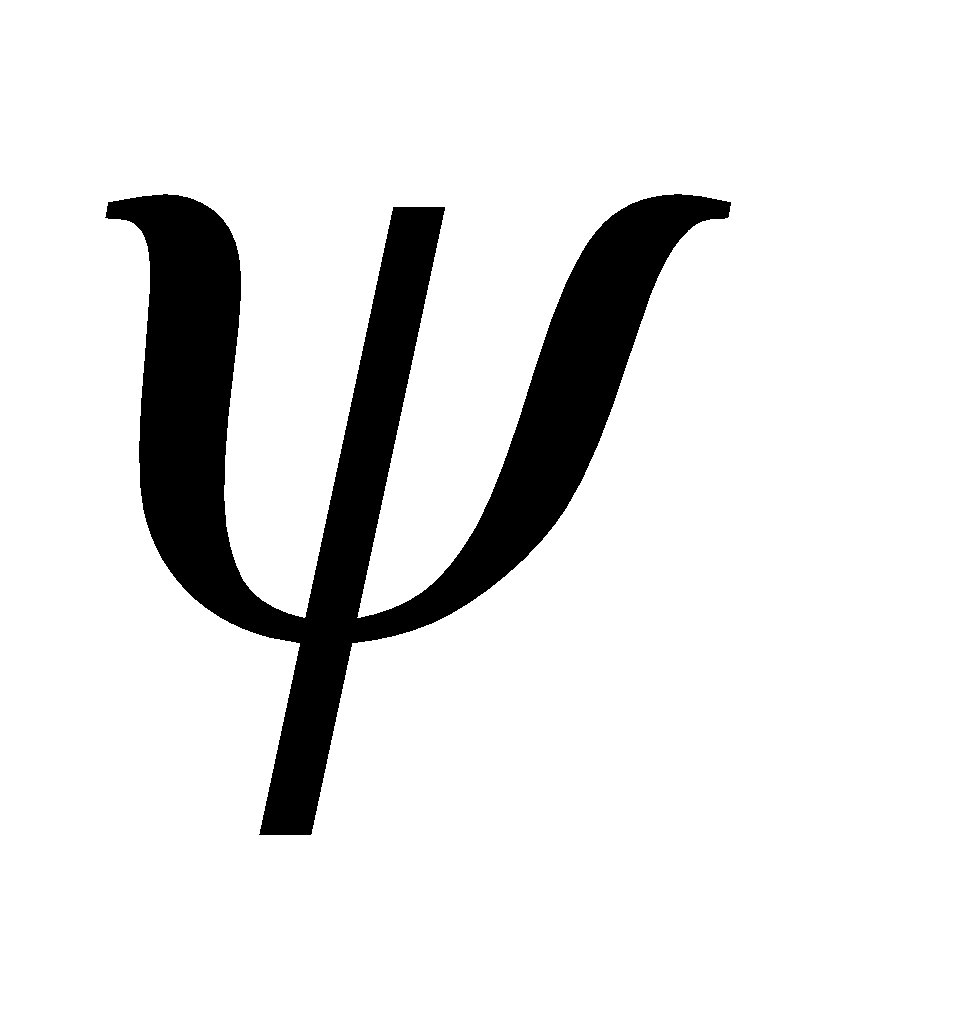
is the angle which a star makes at rising with the horizon, prove that 3
is the angle which a star makes at rising with the horizon, prove that 3
Where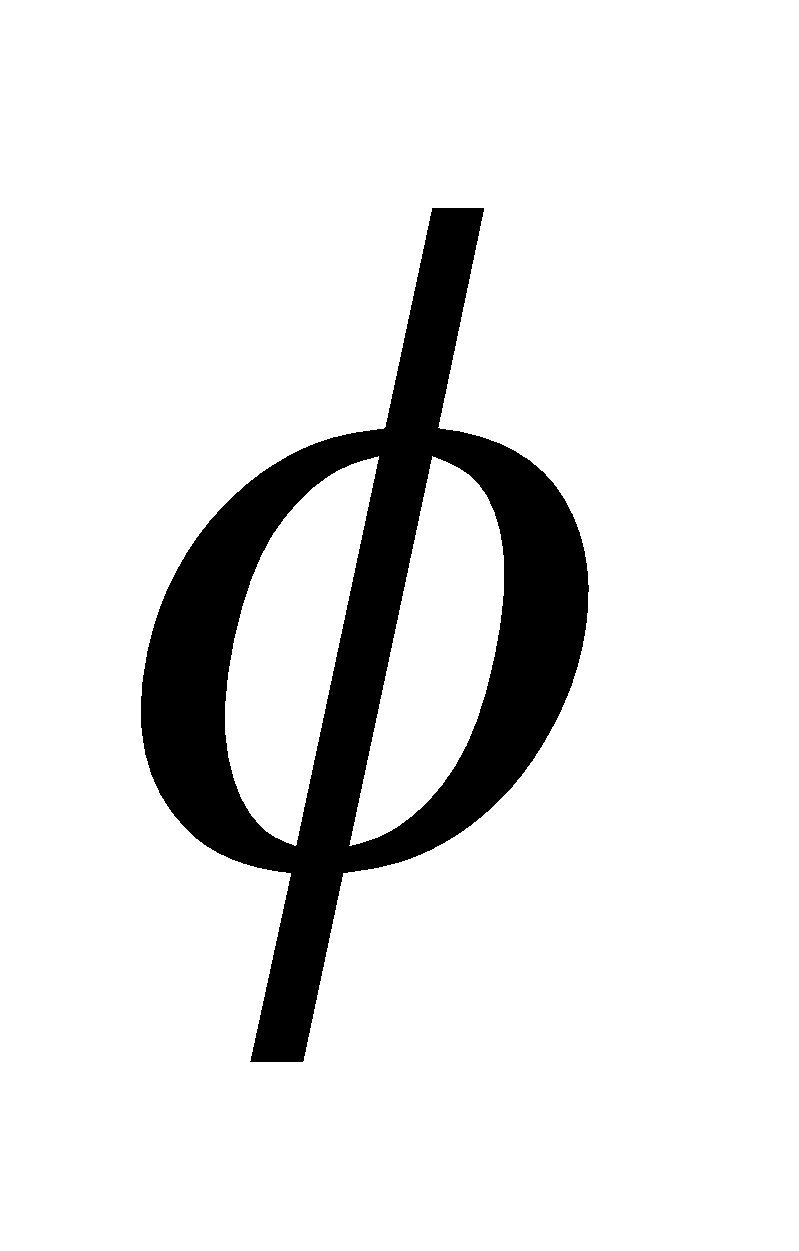 
and 
have their own meanings.
and have their own meanings.
9. State three Kepler’s laws. 3
10. Define the following (any two): 1x2=2
- Aphelion.
- Eccentric anomaly.
- True anomaly.
11. Derive an expression for the position of a body in an elliptic orbit. 5
Or
If
and
are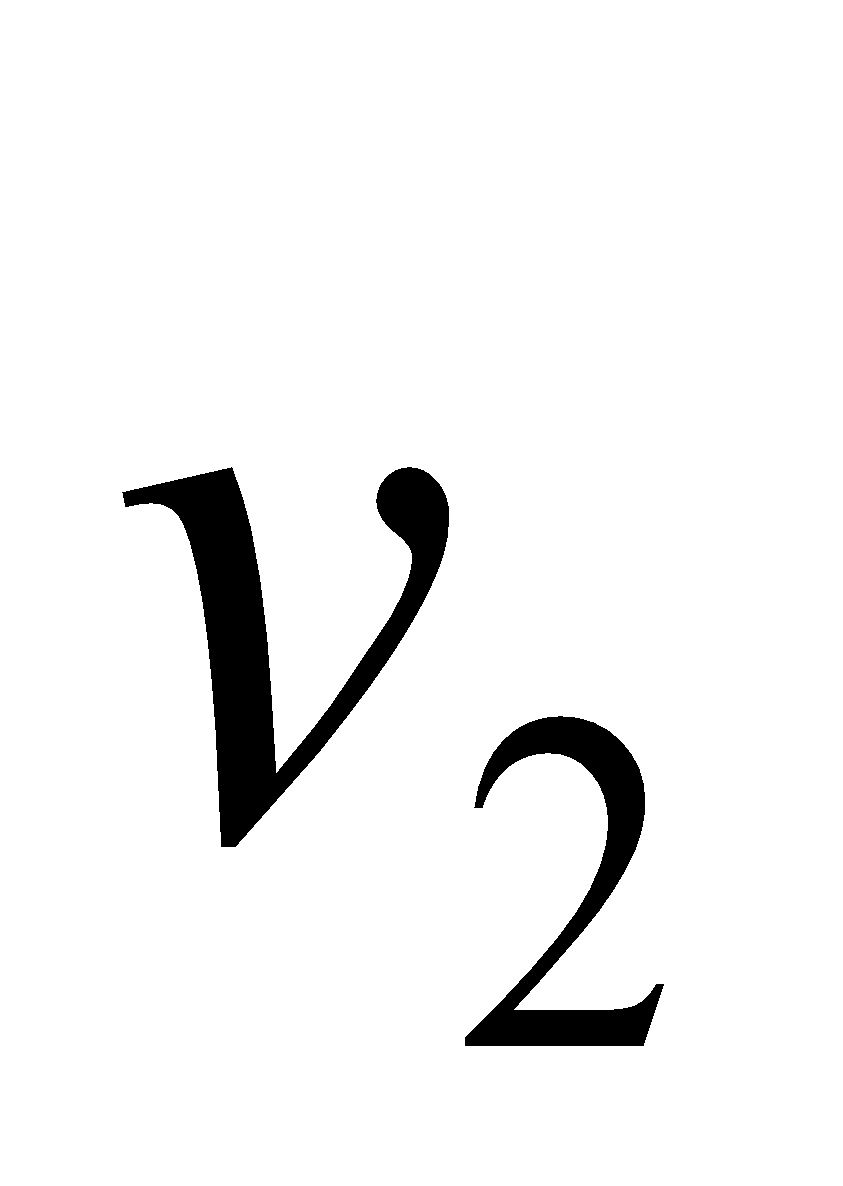 linear velocities of a planet at perihelion and aphelion respectively, prove that
andare linear velocities of a planet at perihelion and aphelion respectively, prove that 
(b) Relativity
(Marks: 40)
12. What is an inertial frame of reference? Can earth be considered as an inertial frame of reference in true sense? Justify. 1+1=2
13. When does Lorentz transformation reduce to Galilean transformation? 1
14. Choose the correct answer: 1
If the interval of occurrence of two events is space-like, then there exists a frame of reference in which two events occur
- At the same time.
- At a finite interval of time.
- At an infinite interval of time.
15. State the two postulates of special theory of relativity. 2
16. Write short notes on the following: 3+2=5
- Length contraction.
- Relative simultaneity.
17. (a) A particle with a mean proper lifetime of 2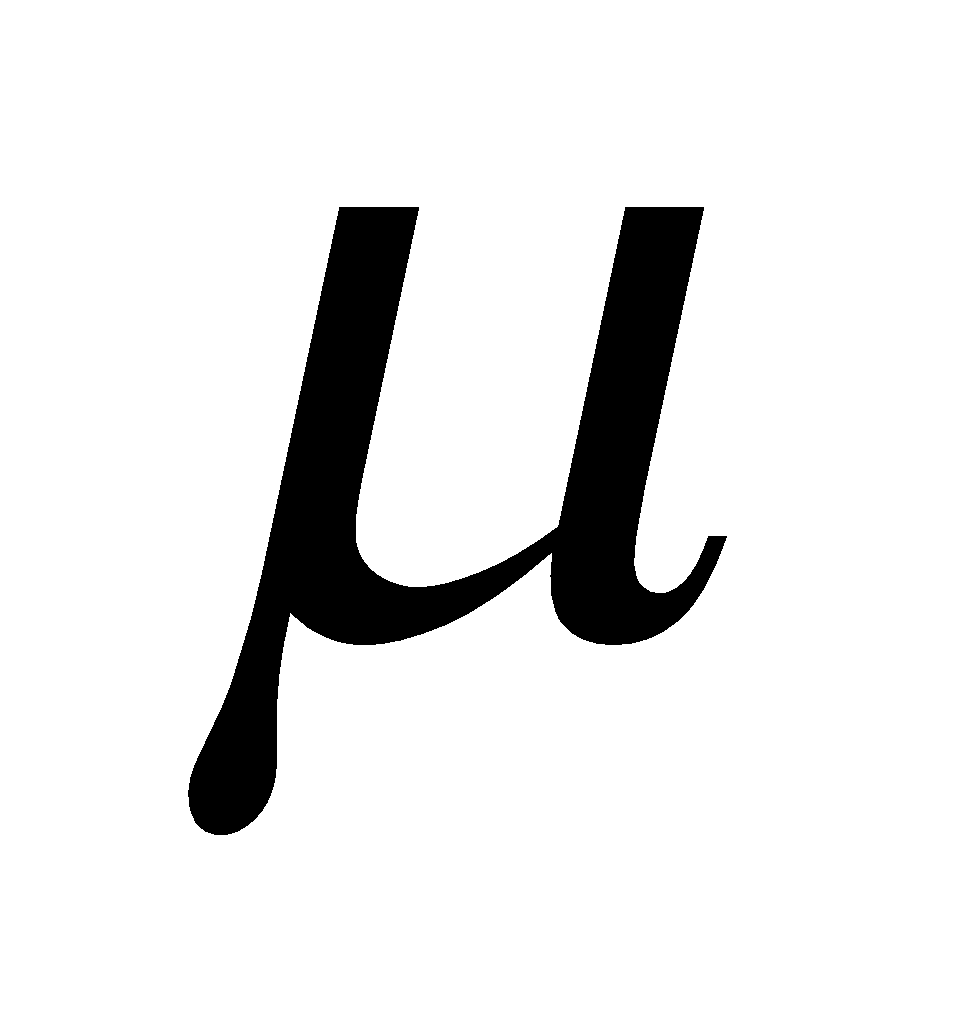
sec moves through the laboratory with a speed of 0.9c. Calculate its lifetime as measured by an observer in the laboratory. 3
sec moves through the laboratory with a speed of 0.9c. Calculate its lifetime as measured by an observer in the laboratory. 3
(b) The length of a rocket ship is 100 m on the ground. When it is in flight, its length observed on the ground is 99 m. calculate its speed. 3
(c) A scientist observes that a certain atom A moving relative to him with velocity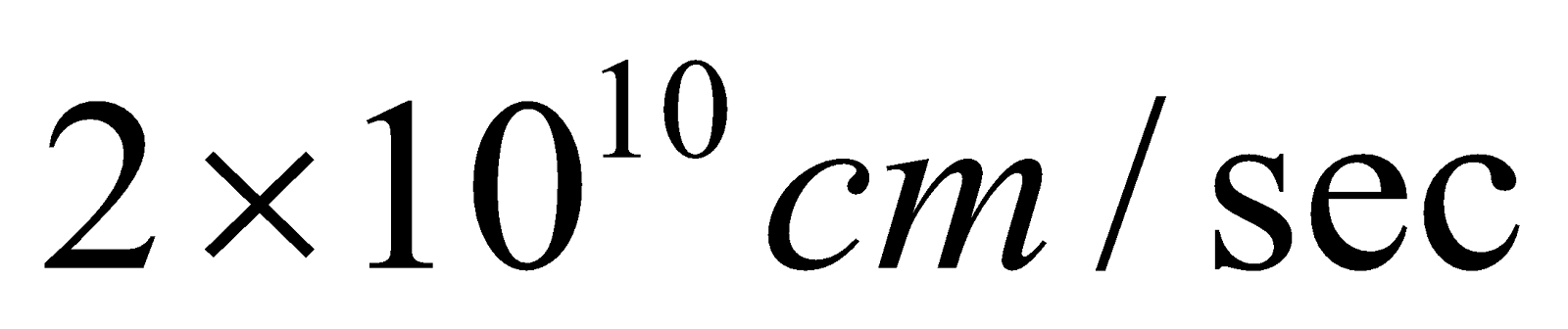 
emits a particle B which moves with velocity 
with respect to the atom. Calculate the velocity of the emitted particle relative to the scientist. 3
emits a particle B which moves with velocity with respect to the atom. Calculate the velocity of the emitted particle relative to the scientist. 3
18. Establish the relation of variation of mass with velocity.
Where
is the velocity of the body when its mass is
and 
is the mass of body at rest? 6
is the velocity of the body when its mass isand is the mass of body at rest? 6
Or
Establish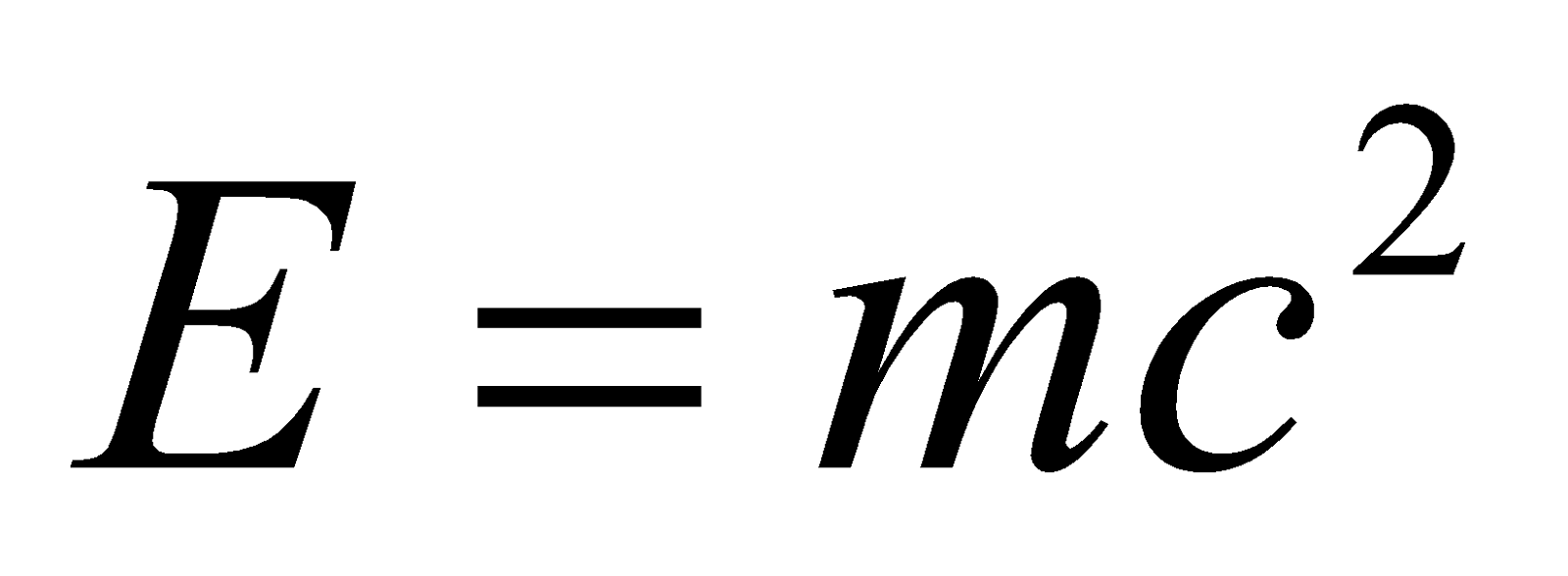 
with usual notations.
with usual notations.
19. What is the increase in the relativistic mass of a particle of rest mass 1 g when it is moving with 0.8c velocity? Hence, find its kinetic energy. 2
20. Answer any two questions: 6x2=12
- Find the transformation laws of density in relativistic mechanics.
- Deduce Lorentz transformation equations.
- Calculate the velocity of an electron having a total energy of 2 MeV.
***
Post a Comment
Kindly give your valuable feedback to improve this website.