2014
(November)
MATHEMATICS
(Major)
Course: 503
(Fluid Mechanics)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
(A) Hydrodynamics
(Marks: 35)
1. (a) State the two methods for studying fluid motion mathematically. 1
(b) Fill in the blank: 1
A ____ is a curve drawn in the fluid such that the tangent to it at every point is in the direction of the vorticity vector
.
.
(c) Define path lines. Write the condition under which streamlines and path lines coincide. 1+1=2
2. (a) Show that
are the velocity components of a possible liquid motion. Is this motion irrotational? 3+3=6
(b) Deduce the equation of continuity in Cartesian coordinate system. 5
Or
The particles of a fluid move symmetrically in space with regard to a fixed centre. Prove that the equation of continuity is
where 
is the velocity at distance 
and 
is the density of fluid particle.
is the velocity at distance and is the density of fluid particle.
3. (a) Write down the Bernoulli’s equation for steady and irrotational flow.
(b) Liquid is contained between two parallel planes; the free surface is a circular cylinder of radius
, whose axis is perpendicular to the planes. All the liquid within a concentric circular cylinder of radius 
is suddenly annihilated. Prove that, if 
be the pressure at the outer surface, the initial pressure at any point of the liquid at distance 
from the centre, is
, whose axis is perpendicular to the planes. All the liquid within a concentric circular cylinder of radius is suddenly annihilated. Prove that, if be the pressure at the outer surface, the initial pressure at any point of the liquid at distance from the centre, is 
5
4. Deduce Euler’s dynamical equations of motion in Cartesian coordinates. 6
Or
A portion of homogeneous fluid is confined between two concentric spheres of radii. A and a, and is attracted towards their centre by a force varying inversely as square of the distance. The inner spherical surface is suddenly annihilated, and when the radii of the inner and outer surface of the fluid are r and R, the fluid impinges on a solid ball concentric with their surfaces. Prove that the impulsive pressure at any point of the ball for different values of R and r varies as
5. (a) Deduce from Green’s theorem that the total flow of liquid into any closed region at any instant is zero. 2
(b) State and prove Kelvin’s minimum energy theorem. 6
Or
In an irrotational motion is two dimensions, prove that
where 
denotes the fluid velocity.
denotes the fluid velocity.
(B) Hydrostatics.
(Marks: 45)
6. (a) Write True or False: 1
When two fluids of different densities at rest under gravity do not mix their surface of separation is a horizontal plane.
(b) If 
be the weight of a given substance in dynes, 
its density in gm per cubic cm, 
its volume in cubic cm, and 
the acceleration of gravity measured in cm/second/second, then show that 
. 2
be the weight of a given substance in dynes, its density in gm per cubic cm, its volume in cubic cm, and the acceleration of gravity measured in cm/second/second, then show that . 2
(c) Show that in a homogeneous liquid at rest under gravity, the difference between the pressures at two points varies as the vertical distance between them. 2
7. (a) A mass of fluid is at rest under the action of given forces. Obtain the differential equation that determines the pressure at any point of the fluid. 6
Or
Prove that the pressure at any point of a fluid at rest under gravity is the same in all directions.
(b) A tube in the form of a parabola held with its vertex downwards and axis vertical, is filled with two different liquids of densities 
and
. If the distances of the free surfaces of the liquids from the focus are 
and 
respectively, show that the distance of their common surface from the focus is
and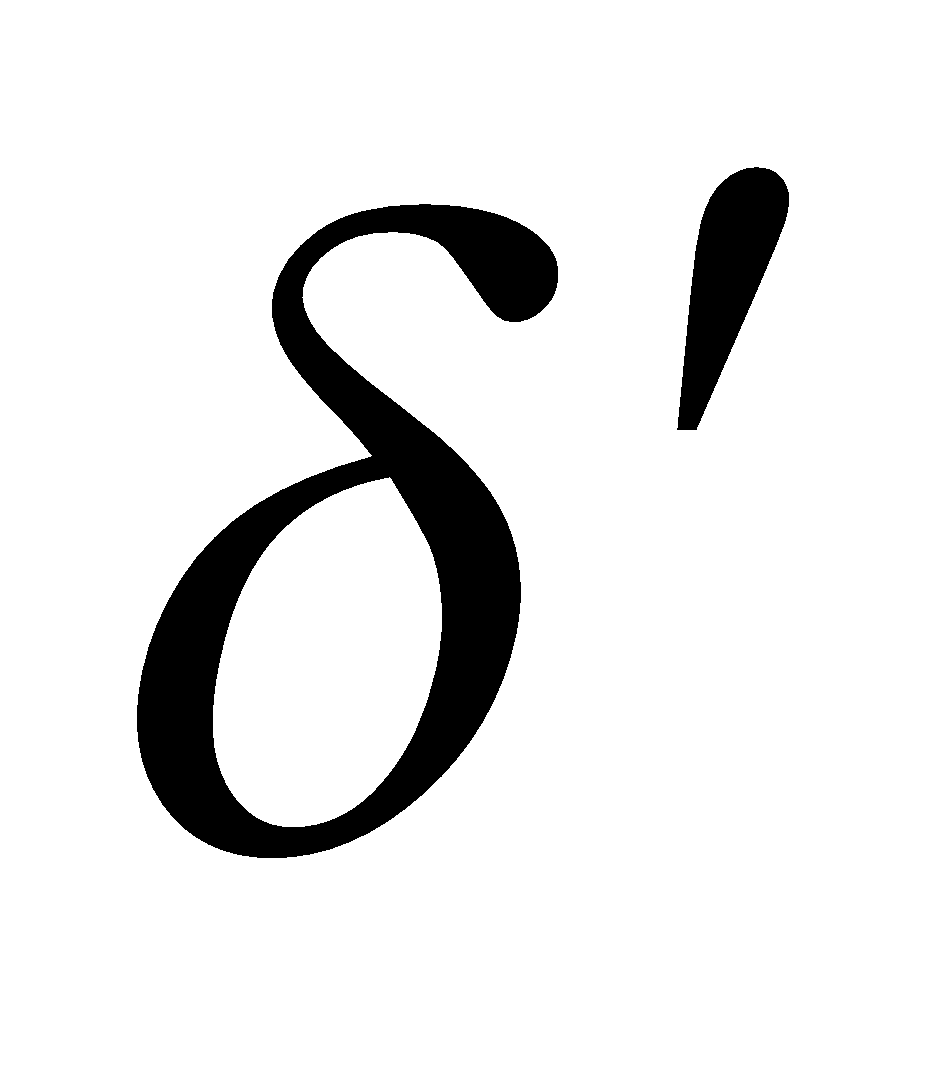. If the distances of the free surfaces of the liquids from the focus are and respectively, show that the distance of their common surface from the focus is 
6
Or
A mass of fluid is at rest under the forces
Find the density and prove that the surfaces of equal pressure are hyperboloids of revolution.
8. (a) Fill in the blank: 1
The depth of the ____ of a plane area immersed in a liquid is greater than the depth of the centre of gravity.
(b) Define force of buoyancy and centre of buoyancy. 2
9. (a) Find the centre of pressure of a triangular area immersed in a homogeneous liquid with its vertex in the surface and base horizontal. 6
Or
A semi-circular lamina is immersed in a liquid with the diameter in the surface. Find the depth of the centre of pressure.
(b) A hemispherical bowl is filled with water and inverted, and placed with its plane base is contact with a horizontal table. Find the resultant thrust on its surface. Also show that the resultant vertical thrust on its surface is one-third of the thrust on the table. 7
Or
A rectangular area is immersed in a heavy homogeneous liquid with two sides horizontal and is divided by horizontal lines into strips on which the total thrusts are equal. If a, b, c are the breadths of three consecutive strips, prove that 
10. (a) Define metacentre. 1
(b) Fill in the blank:
If the ____ coincides with the centre of gravity, the equilibrium is neutral. 1
(c) A body floats partly immersed in one-liquid and partly in another. Find the condition of equilibrium. A body floating in water has volumes 
above the surface when the densities of the surrounding air are respectively 
, show that
above the surface when the densities of the surrounding air are respectively , show that 
4
11. If the floating solid is a cylinder, with its axis vertical, the ratio of whose specific gravity to that of the fluid is 
, prove that the equilibrium will be stable, if the ratio of the radius of the base to the height is grater than 
. 6
, prove that the equilibrium will be stable, if the ratio of the radius of the base to the height is grater than . 6
Or
A solid cone, of semi-vertical angle
, specific gravity 
floats in equilibrium in the liquid of specific gravity 
with its axis vertical and vertex downwards. Determine the condition for which the equilibrium is stable.
, specific gravity floats in equilibrium in the liquid of specific gravity with its axis vertical and vertex downwards. Determine the condition for which the equilibrium is stable.
***
Post a Comment
Kindly give your valuable feedback to improve this website.