[BA 4th Sem Question Papers, Dibrugarh University, 2013, Mathematics, Major, A: Linear Programming, B: Analysis - II]
1. (a) How many basic assumptions are necessary for all linear programming models? 1
(b) Write the general linear programming problem with 
decision variables and 
constraints. 2
decision variables and constraints. 2
(c) A company makes 3 models of calculator – A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculators of model B and 4800 calculators of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made everyday. It costs Rs. 12,000 and Rs. 15,000 each day to operate factory I and II respectively. Find the number of days each factory should operate to minimize the operating costs and still meet the demand. 3
(d) Solve graphically the following LPP: 4
Maximize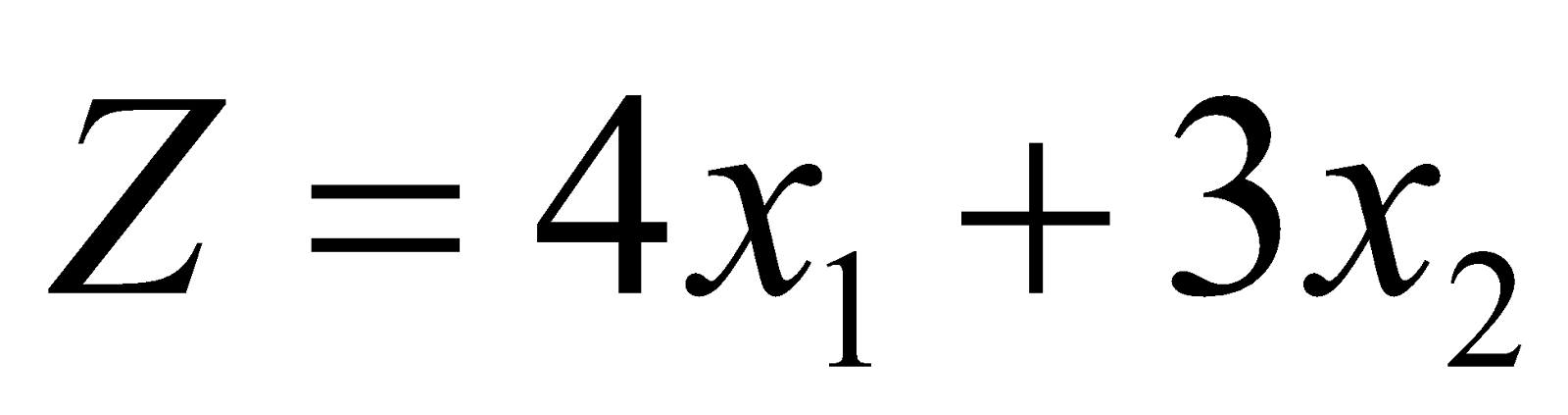
Subject to the constraints
2. (a) For what reasons, additional variables are to be addend to convert an LPP into standard form? 2
(b) Solve by simplex method: 5
Maximize
Subject to the constraints
(c) Solve by two-phase method: 8
Maximize
Subject to the constraints
Or
Solve by Big-M method:
Maximize
Subject to the constraints
3. (a) What happens in the dual if the variables in primal in unrestricted in sign? 1
(b) Fill up the blank: 1
“If the primal problem has an unbounded objective function, then the dual has ____ solution.”
(c) Write two rules for constructing the dual from the primal. 2
(d) Find the dual of the following primal LPP: 4
Minimize
Subject to the constraints
Unrestricted in sign.
Or
Prove that the dual of the dual linear programming problem is the primal.
4. (a) What is the necessary and sufficient condition for the existence of a feasible solution to the transportation problem? 1
(b) Mention two properties of a loop in a transportation problem. 2
(c) Obtain an optimal solution to the following transportation problem by Vogel’s method: 9
 |  |  |  |
Supply
| |
 |
19
|
30
|
50
|
10
|
7
|
 |
70
|
30
|
40
|
60
|
9
|
 |
40
|
8
|
70
|
20
|
18
|
Demand
|
5
|
8
|
7
|
14
|
34
|
Or
What do you mean by balanced transportation problem? Find the initial basic feasible solution of the following problem with the help of least cost method:
| | | |
Supply
| |
|
1
|
2
|
1
|
4
|
30
|
|
3
|
3
|
2
|
1
|
50
|
|
4
|
2
|
5
|
9
|
20
|
Demand
|
20
|
40
|
30
|
10
|
B: ANALYSIS – II
(Multiple Integral)
(Marks: 35)
5. (a) When will the trigonometric series be a Fourier series? 1
(b) For a periodic function of period
, show that 2
, show that 2
Where
is any number?
is any number?
(c) If the function
is periodic with period
on the interval
, then find the Fourier series of
. 3
is periodic with periodon the interval, then find the Fourier series of. 3
(d) Obtain the Fourier series of the periodic function
with period
defined as 4
with perioddefined as 4
And hence deduce that
Or
If a function
is bounded, periodic with period
and integrable on
and piecewise monotonic on
, then prove that
is bounded, periodic with periodand integrable onand piecewise monotonic on, then prove that 
Where
,
are Fourier coefficients of
.
,are Fourier coefficients of.
6. (a) Write the parametric representation of the curve
1
1
(b) If a function
is defined as
is defined as 
Then show that
3
(c) Evaluate
Over the region
4
Or
Evaluate
Over the region
Where
(d) State and prove Green’s theorem. 5
Or
Using Green’s theorem, compute the difference between the line integrals.
And
Where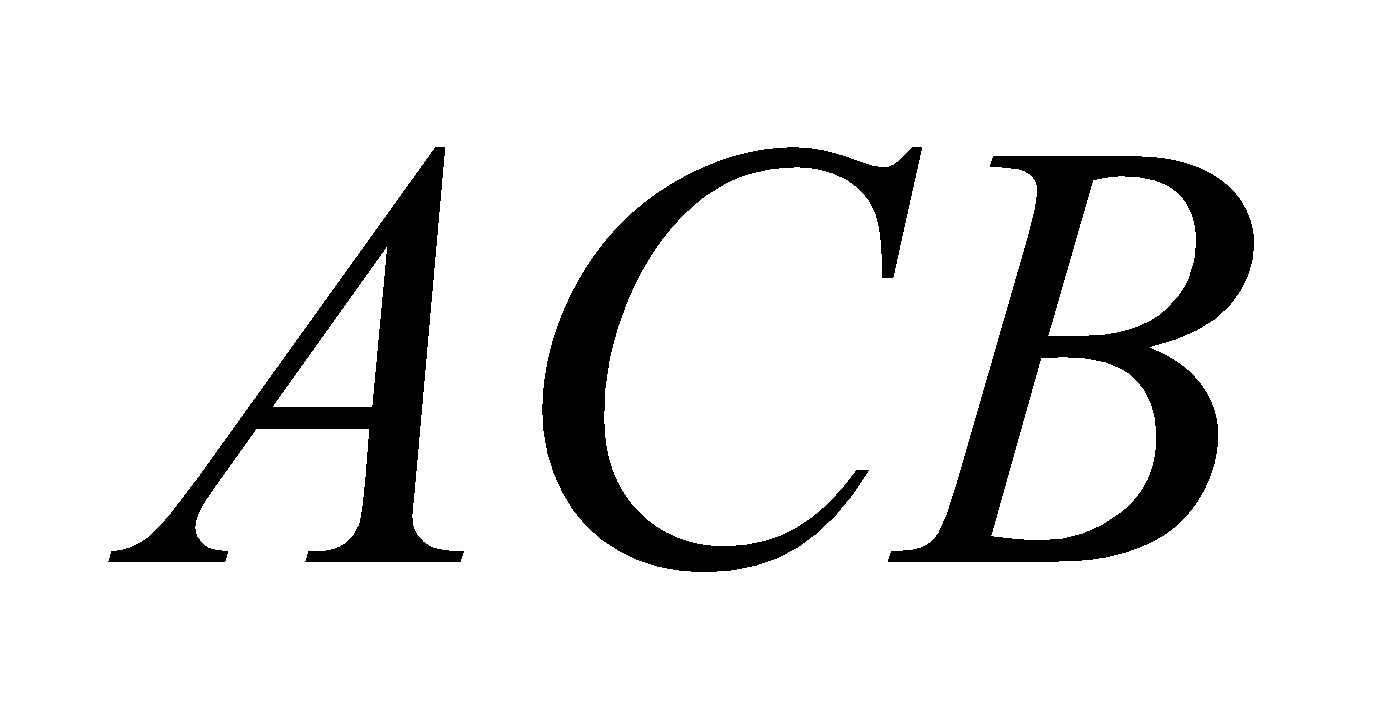
and
are respectively the straight line
and the parabolic are
, joining the points
and
.
andare respectively the straight lineand the parabolic are, joining the pointsand.Also Read: Dibrugarh University Question Papers
7. (a) Define a surface in
1
1
(b) State Gauss’ theorem. 1
(c) Evaluate 
2
2
Where
is the outer side of the part of the sphere
4
is the outer side of the part of the sphere 4
Or
Find the volume of the solid bounded by the surface
and the plane
and the plane
(d) Using Stokes’ theorem, show that 5
Where
is the portion of the surface
is the portion of the surface
Or
Using Gauss’ theorem, show that
Where
is the closed surface bounded by the cone
and the plane
and
,
,
are direction cosines of the outward drawn normal of
.
is the closed surface bounded by the coneand the planeand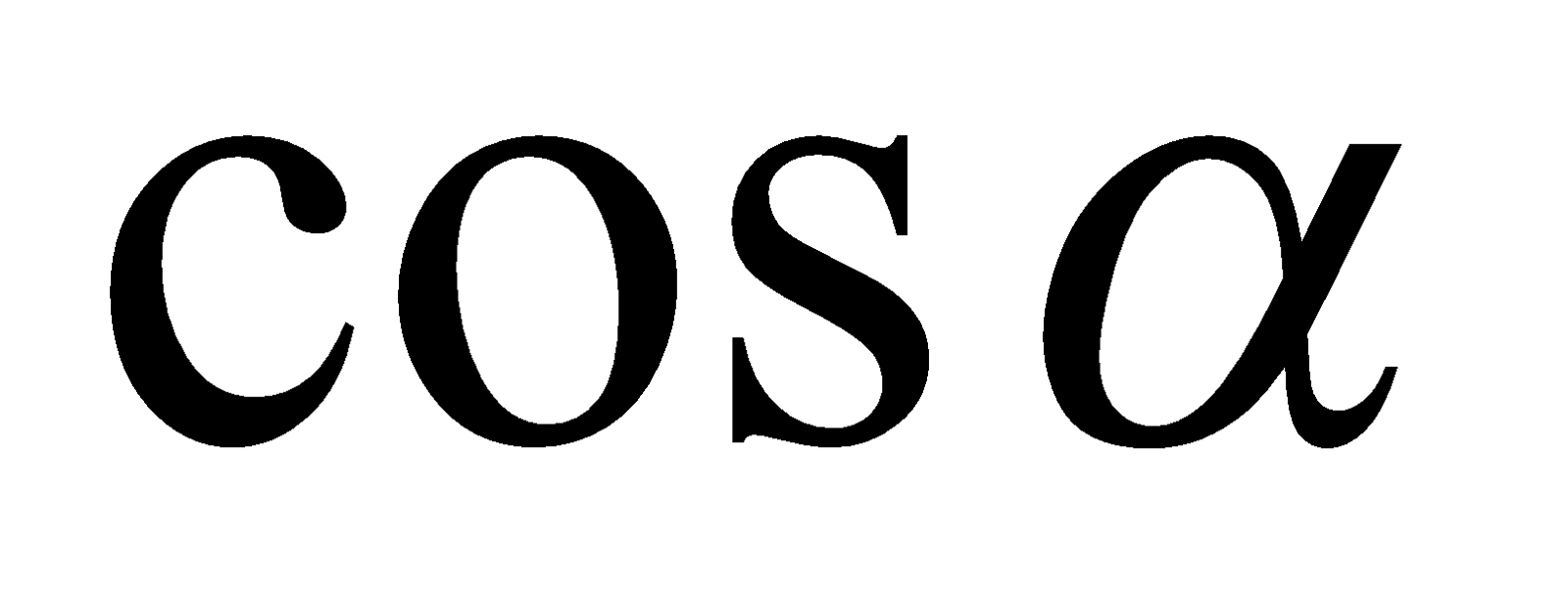,,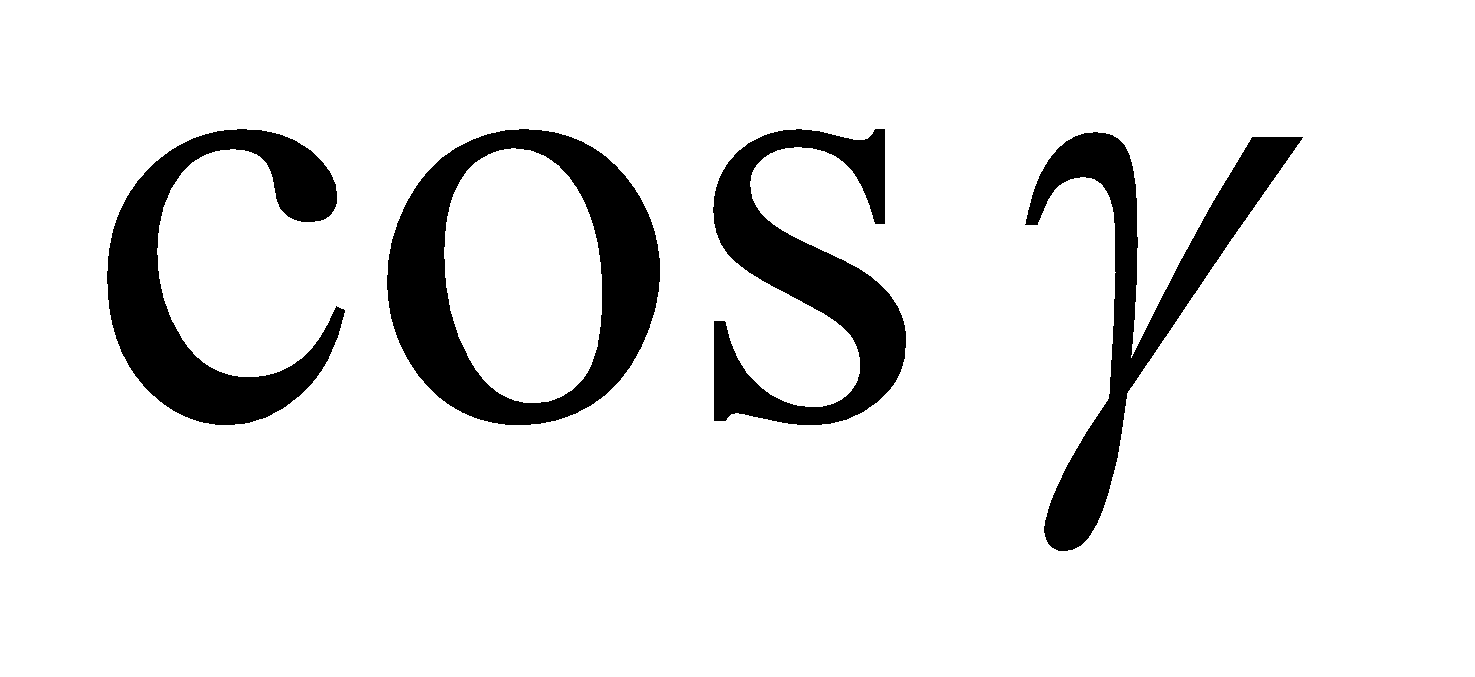are direction cosines of the outward drawn normal of.
***
Post a Comment
Kindly give your valuable feedback to improve this website.