2015
(November)
MATHEMATICS
(General)
Course: 501
[(A) Analysis – II, (B) Mechanics]
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
1. (a) Write when the limit of a complex function exists. 1
(b) Prove that 
is continuous at 
. 3
is continuous at . 3
Or
Show that 
is non-analytic 3
is non-analytic 3
(c) State and prove the necessary condition for a function to be analytic.
Or
If 
, then find 
, such that 
is analytic.
, then find , such that is analytic.
2. (a) Derivative of an analytic function is not analytic. State true or false.
(b) Prove that
.
.
(c) State and prove Cauchy’s integral formula.
Or
Evaluate 
along the curve 
given by the line from 
to 
and the line from to
.
along the curve given by the line from to and the line from to.
(d) Define complex line integral. 3
3. (a) Write the condition for the convergence of the Taylor’s series. 1
(b) Find the singularity of the function
. 3
. 3
(c) Find the residue of any one of the following: 3
at
at
(d) Evaluate any one of the following by using contour integration: 6
(B) Mechanics
(Marks: 45)
(a) Statics
4. (a) Define screw.
(b) Write the name used for denoting a single reduced force and a couple of a system of forces.
(c) Write the conditions that the system of coplanar forces may be in equilibrium.
(d) Find the equation of a system of coplanar forces acting at different points of a rigid body.
Or
Show that any system of forces acting on a rigid body can be reduced to a single force together with a couple whose axis is along the direction of the force.
5. (a) Define virtual displacement. 1
(b) Define span of a common catenary. 1
(c) Write two forces which can be omitted while writing the equation of virtual work. 2
(d) State and prove the principle of virtual work for a system of coplanar forces. 6
(b) Dynamics
6. (a) Define angular velocity of a point. 1
(b) Simple harmonic motion of a particle is described by
. Find the time period.
. Find the time period.
(c) Find the tangential and normal components of velocity of a moving point along a plane curve. 5
Or
A particle describes the curve 
with a constant velocity. Find the components of velocity along the radius vector and perpendicular to it.
with a constant velocity. Find the components of velocity along the radius vector and perpendicular to it.
7. (a) Define central orbit. 1
(b) A particle describes a curve 
under a force 
to the pole. Find the law of force. 6
under a force to the pole. Find the law of force. 6
Or
A particle is projected upwards under gravity in a resisting medium, whose resistance varies as the square of the velocity. Find the velocity of the particle at any position. 6
8. (a) State the theorem of parallel axes of moment. 2
(b) Define radius of gyration. 2
(c) Find the moment of inertia of a uniform rod of length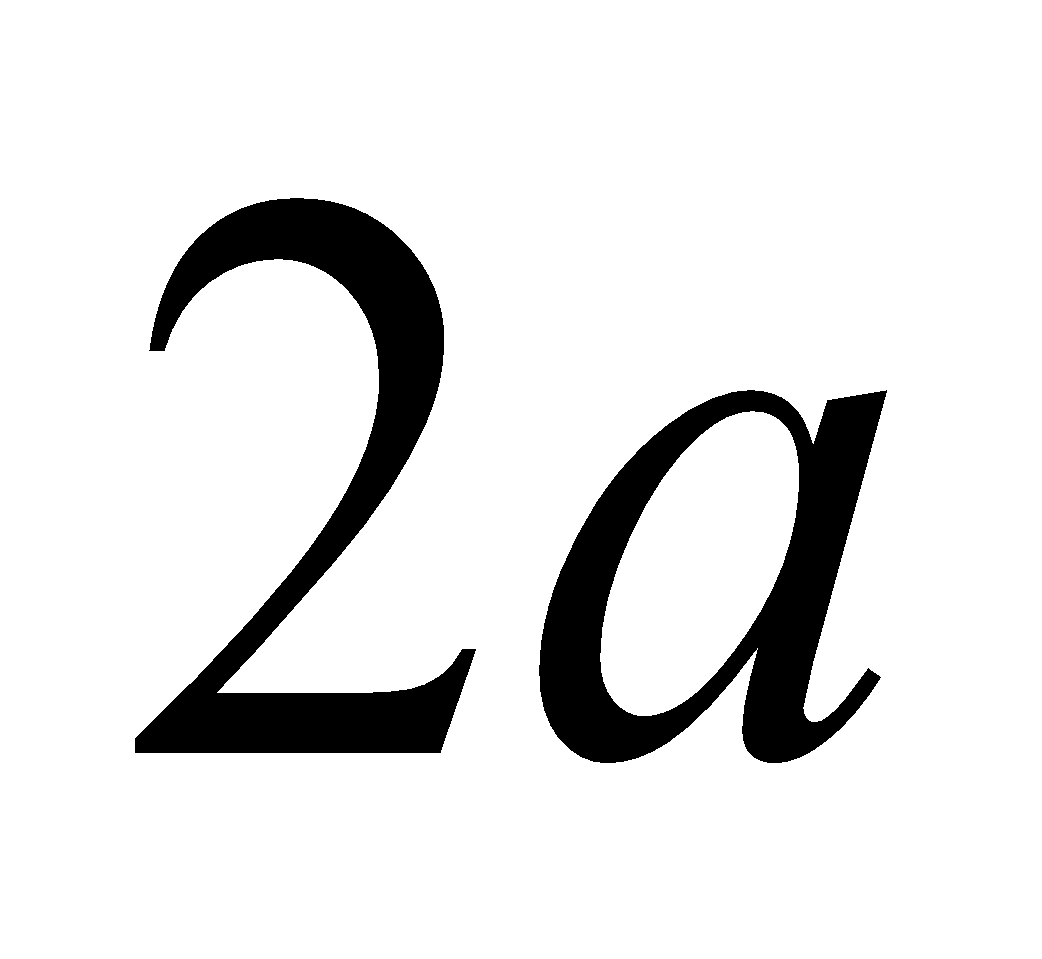 
and mass 
about an axis through the middle point and perpendicular to it. 6
and mass about an axis through the middle point and perpendicular to it. 6
***
Post a Comment
Kindly give your valuable feedback to improve this website.