2015
(November)
MATHEMATICS
(Major)
Course: 501
(Logic and Combinatorics, and Analysis - III)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
(A) Logic and Combinatorics
(Marks: 35)
1. (a) Define a truth function. 1
(b) Let
: Ice is cold, 
: Blood is green. Write the following sentences in symbolic form: 2
: Ice is cold, : Blood is green. Write the following sentences in symbolic form: 2- Either ice is cold or blood is green.
- If blood is green then ice is not cold.
(c) Prove that 
is a tautology. 3
is a tautology. 3
(d) Prove that every statement can be generated by 
only. 4
only. 4
Or
Prove that 
is a valid statement. 4
2. (a) Write the law of syllogism. 1
(b) Using predicates, write the following sentences in symbolic form: 2
- All teachers like all students.
- Only teachers like students.
(c) Test the validity of the following arguments: 3
All squares have equal sides.
A rhombus has equal sides.
Therefore, a rhombus is a square.
(d) Prove that 
is a valid consequence of the following premises: 4
is a valid consequence of the following premises: 4
Or
All men are mortal.
Ram is a man.
Hence Ram is mortal.
Write the formal derivation.
3. (a) Write the fundamental principles of counting. 1
(b) A computer password consists of a letter of the alphabet followed by 3 or 4 digits. Find the total number of passwords that can be formed. 2
(c) Define Catalan number. Prove that the nth Catalan number defined from 
to 
is given by 
1+3=4
to is given by 1+3=4
Or
Define Stirling number of first kind. Find the number of functions from a set 
of 
elements to a set 
of 
elements such that the ranges of these functions have exactly 
elements each. 4
of elements to a set of elements such that the ranges of these functions have exactly elements each. 4
4. (a) Write the Pigeonhole theorem. 1
(b) Prove that given any 12 natural numbers, one can choose 2 of them such that their difference is divisible by 11. 3
(c) Find the number of solutions in integers of the equation 4
Or
Use generating functions to find the number of ways to select 
objects of 
different kinds if we must select at least one object of each kind. 4
objects of different kinds if we must select at least one object of each kind. 4
(B) Analysis – III (Complex Analysis)
(Marks: 45)
5. (a) Define continuity of a function of a complex variable. 1
(b) If
Then prove that 
is not differentiable at
. 3
is not differentiable at. 3
(c) Prove that the function
is not analytic at 
, although Cauchy-Riemann equations are satisfied at that point. 6
, although Cauchy-Riemann equations are satisfied at that point. 6
Or
Prove that 
is harmonic. Find its harmonic conjugate. 6
is harmonic. Find its harmonic conjugate. 6
6. (a) Define Jordan arc. 1
(b) Evaluate 
along the path 1
along the path 1 
(c) State and prove Liouville’s theorem. 5
(d) Answer the following (any one): 4
- Using Cauchy integral formula, evaluate
where 
is the circle 
.
is the circle .- Evaluate
, where
is given by
.
7. (a) Define radius of convergence of a power series. 2
(b) Expand 
in the region
. 3
in the region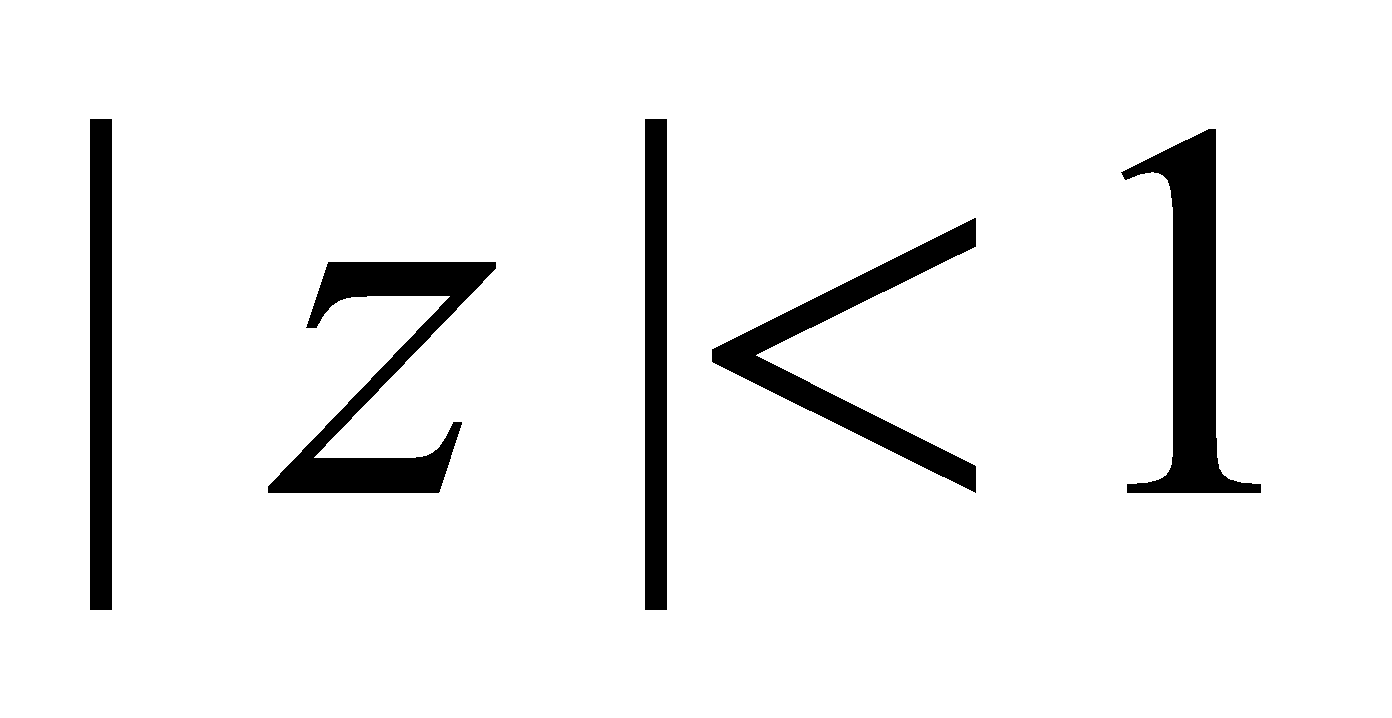. 3
(c) Expand 
in a Taylor’s series about 
3
in a Taylor’s series about 3
Or
Expand 
for
. 3
for. 3
8. (a) Define isolated singular point. 1
(b) Find the poles of
. 2
. 2
(c) Evaluate (any two): 5x2=10
***
Post a Comment
Kindly give your valuable feedback to improve this website.