2015
(November)
MATHEMATICS
(Major)
Course: 503
(Fluid Mechanics)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
(A) Hydrodynamics
(Marks: 35)
1. (a) Write the equation of path line. 1
(b) In a motion velocity potential is single valued, then write the nature of the motion. 1
(c) If vorticity vector of every fluid particle is zero, then write the nature of the motion. 1
(d) Define vorticity vector. 2
(e) Write the differences between streamlines and path lines. 3
(f) Derive the equation of continuity of fluid flow by Euler’s method. 7
Or
Find the equation of streamlines for the flow  at the point
at the point . 7
. 7
2. (a) State True or False: 1
Impulsive pressure at any point in a fluid is the same in every direction.
(b) State Kelvin’s circulation theorem. 1
(c) Derive Bernoulli’s equation of motion of fluid. 7
Or
Derive Euler’s equation of motion. 7
(d) A velocity field is given by
Find the stream function at  . 3
. 3
3. (a) Using Green’s theorem, find the expression for kinetic energy T of a liquid. 4
(b) A velocity field is given by
Determine whether the flow is irrotational or not. 4
Or
Show that in irrotational motion the velocity cannot be a maximum in the interior of the fluid. 4
(B) Hydrostatics
(Marks: 45)
4. (a) Define density of a homogeneous substance. 1
(b) Write the entity to which the pressure at any point in a homogeneous liquid is proportional below the effective surface. 1
(c) Find the specific gravity of a mixture of number of substances whose volumes and specific gravities are given. 5
(d) Prove that at rest under gravity, the pressure is same at all points in the same horizontal plane.
5
(e) Show that at rest under gravity horizontal planes are surfaces of equal density. 5
Or
The pressures at two points  and
and 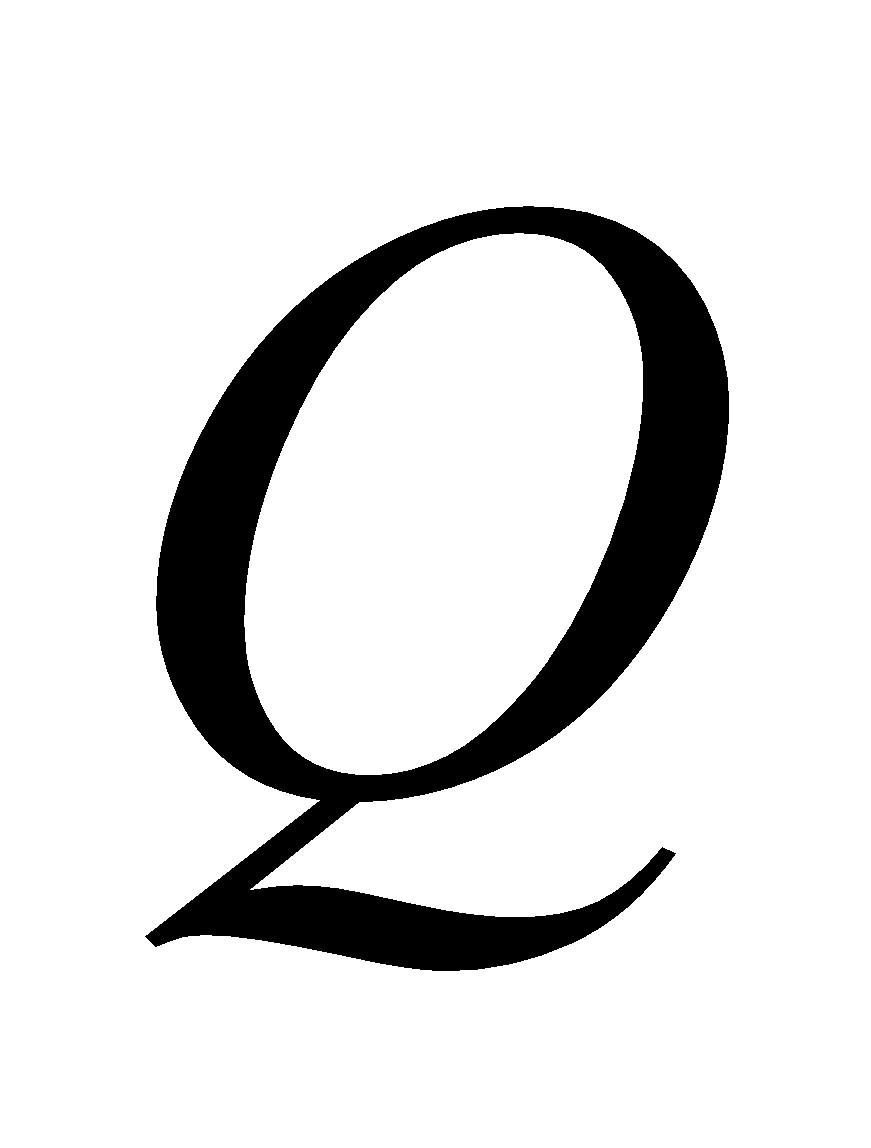 in a homogeneous liquid are
in a homogeneous liquid are  and
and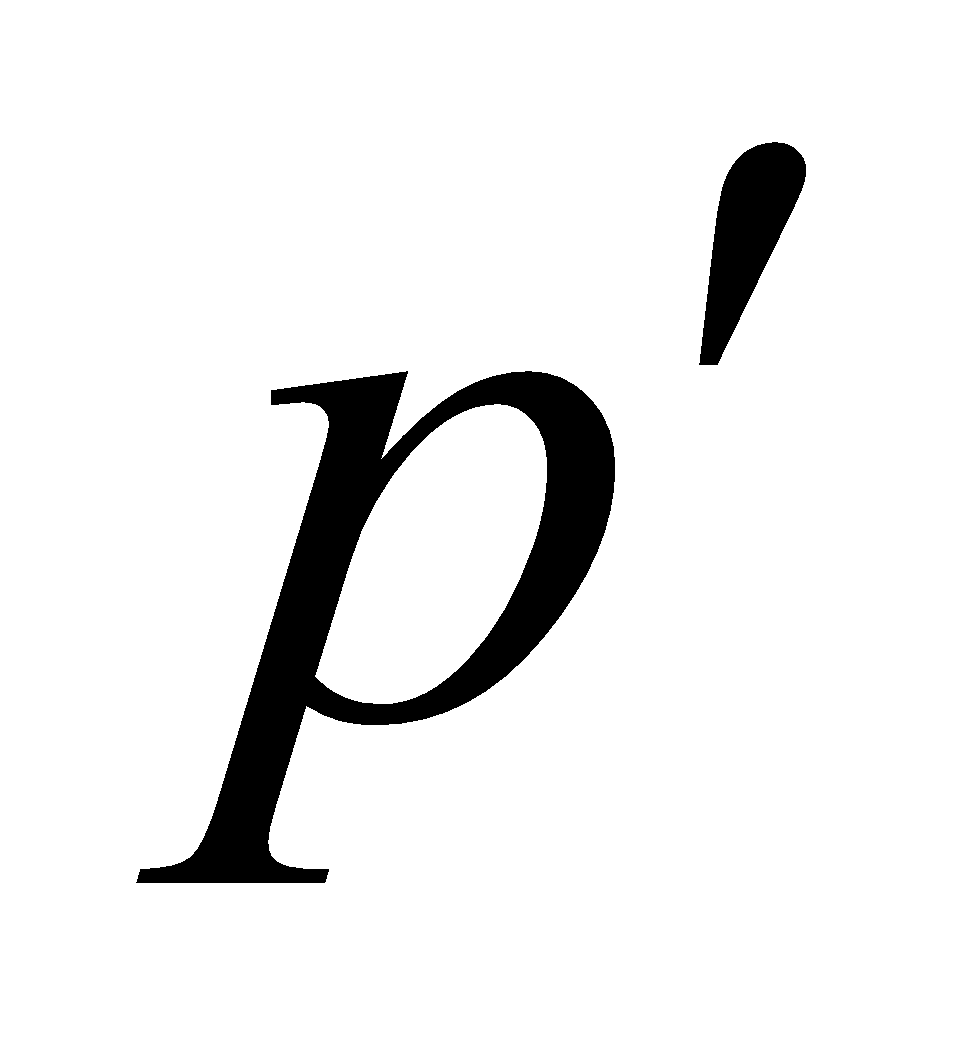 . Prove that the pressure at the point
. Prove that the pressure at the point  which divides
which divides  in the ratio
in the ratio  is
is
5. (a) Define whole pressure. 2
(b) Describe force of buoyancy. 2
(c) Find the centre of pressure of a triangle immersed in a liquid with vertex in the surface and base horizontal. 6
(d) Show that the thrust of a heavy homogeneous liquid on a plane area is the product of the area and the pressure of its centre of gravity, when atmospheric pressure is neglected. 6
Or
A cone full of water is placed on its side on a horizontal table. Show that the thrust on the base is  , where
, where  is the weight of the contained fluid and
is the weight of the contained fluid and  is the vertical angle of the cone. 6
is the vertical angle of the cone. 6
6. (a) Write the conditions of equilibrium for a body floating freely in a homogeneous liquid. 3
(b) Write the forces acting on a body immersed in a liquid and supported by a string. 3
(c) Describe stable, unstable and neutral equilibria of a body immersed in liquid. 6
Or
A thin metallic circular cylinder contains water to a depth  and floats in water with its axis vertical, immersed to a depth
and floats in water with its axis vertical, immersed to a depth . Show that the vertical position is stable if the height of the centre of gravity of the cylinder above its base is less than
. Show that the vertical position is stable if the height of the centre of gravity of the cylinder above its base is less than . 6
. 6
***

Post a Comment
Kindly give your valuable feedback to improve this website.