2014
(November)
MATHEMATICS
(Major)
Course: 504
(Mechanics and Integral Transforms)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
GROUP – A
(MECHANICS)
(Marks: 25)
1. (a) Write the value of the pitch of the wrench 
. 1
. 1
(b) Define screw. 2
(c) Prove that a system of forces can be reduced to a single force acting through an arbitrary chosen point and a couple whose axis passes through that point.
Or
Find the equation of null plane of a given point 
referred to coordinate system
.
referred to coordinate system.
2. (a) Define virtual work.
(b) Write the name of one force which can be omitted in forming the equation of virtual work.
(c) Establish the relation between 
and 
for a common catenary.
and for a common catenary.
(d) State and prove the principle of virtual work for a system of coplanar forces acting at different points of a rigid body.
(e) Derive the intrinsic equation of common catenary. 5
Or
A regular hexagon ABCDEF consists of six equal uniform rods, each of weight w, freely jointed together. The hexagon rests in a vertical plane and AB is in contact with a horizontal table. If C and F be connected by a light string, then find the tension of the string.
(b): Dynamics
(Marks: 25)
3. (a) Define radial velocity of a particle. 1
(b) Define the amplitude of a simple harmonic motion. 1
(c) Find the radial and transverse velocity components of a particle. 6
Or
A particle describes the curve 
with a constant velocity. Find the components of velocity among radius vector and perpendicular to it.
with a constant velocity. Find the components of velocity among radius vector and perpendicular to it.
4. (a) Write the name of the orbit of a particle moving under a central force. 1
(b) If a particle moves upward in a resisting medium, then write the direction along which the resisting force acts. 1
(c) A particle describes the curve 
under a force 
to the pole. Find the law of the force. 5
under a force to the pole. Find the law of the force. 5
Or
A particle falls under gravity from rest in a medium whose resistance varies as the velocity. Find the relation between 
and
.
and.
5. (a) Define effective force on a particle. 1
(b) Let 
be the coordinates of a point mass
. Then write the moment of inertia of the point mass with respect to the origin. 1
be the coordinates of a point mass. Then write the moment of inertia of the point mass with respect to the origin. 1
(c) Prove the theorem of perpendicular axes of moment of inertia. 3
(d) Find the moment of inertia of a plane lamina of length 
and breadth 
about a line through its centre and parallel to
. 5
and breadth about a line through its centre and parallel to. 5
Or
Deduce the general equation of motion of a rigid body from D’Alembert’s principle.
GROUP – B
(INTEGRAL TRANSFORMS)
(Marks: 30)
6. (a) Write the value of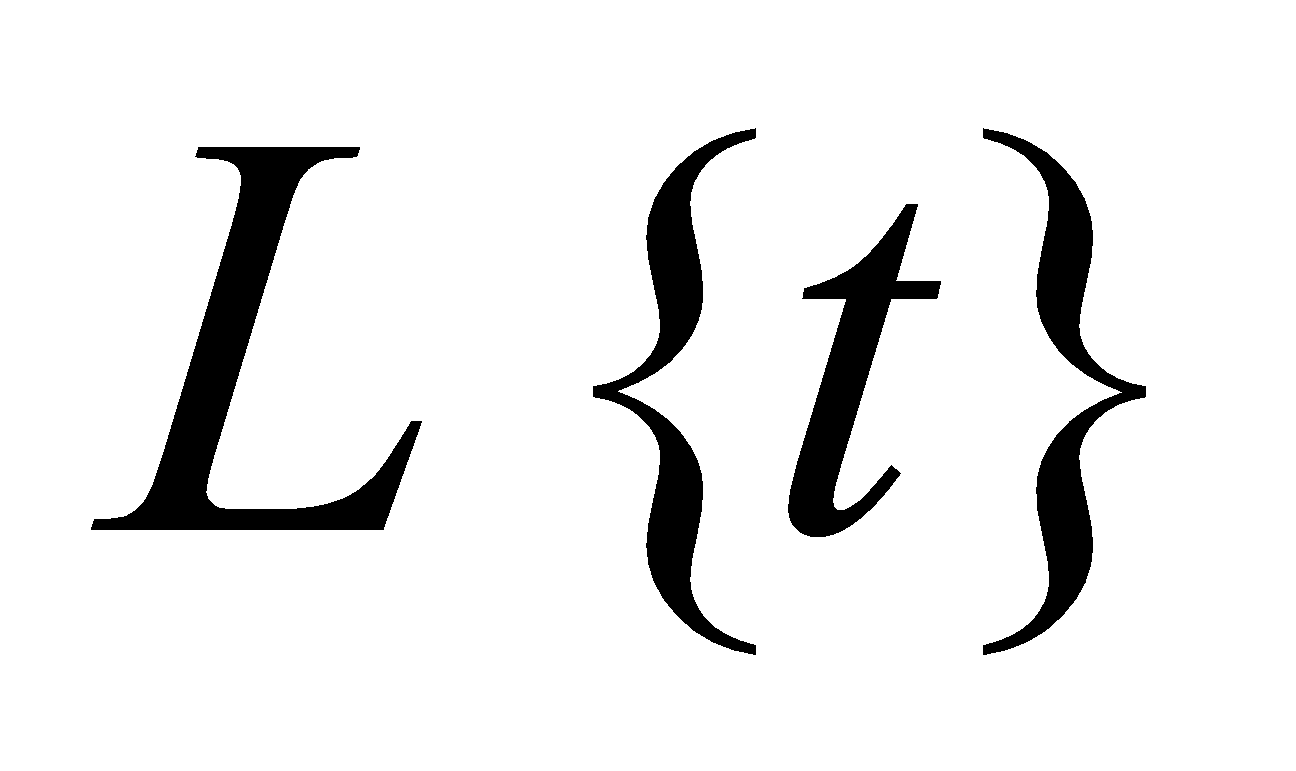 
. 1
. 1
(b) Find
. 2
. 2
(c) Evaluate
. 2
. 2
(d) Evaluate (any one): 3
7. (a) Write the value of 
. 1
. 1
(b) Evaluate: 2+2=4
.
.
(c) Evaluate
. 3
. 3
Or
Evaluate
.
.
8. (a) If 
, then write the value of 
. 1
, then write the value of . 1
(b) Solve 
, using Laplace transform, with conditions 
. 3
, using Laplace transform, with conditions . 3
(c) Solve 
using Laplace transform with conditions
. 5
using Laplace transform with conditions. 5
Or
Solve
, using Laplace transform with conditions
.
, using Laplace transform with conditions.
(d) Solve
using Laplace transform with conditions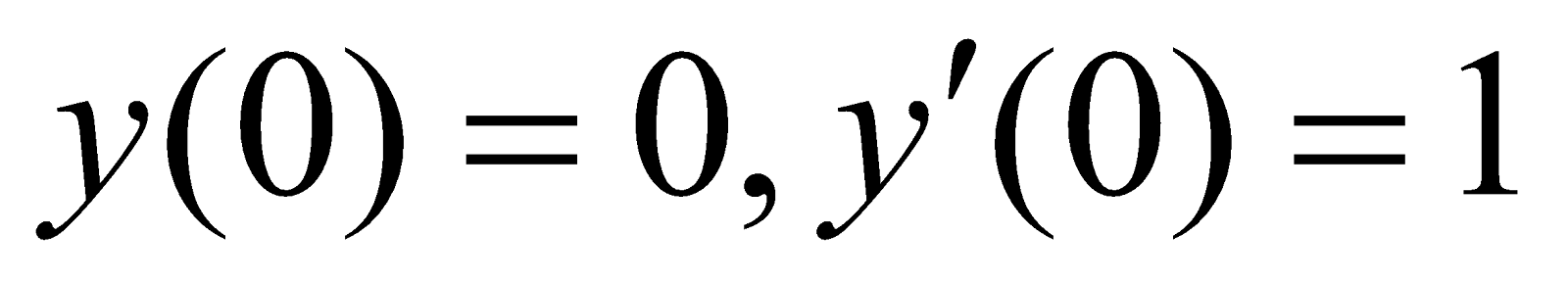 
5
5
Or
Solve 
when 
and
.
when and.
***
Post a Comment
Kindly give your valuable feedback to improve this website.