2015
(May)
MATHEMATICS
(Major)
Course: 601
(A: Metric Spaces and B: Statistics)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions.
A: Metric Spaces
(Marks: 40)
1. (a) Define limit points in a metric space. 1
(b) A mapping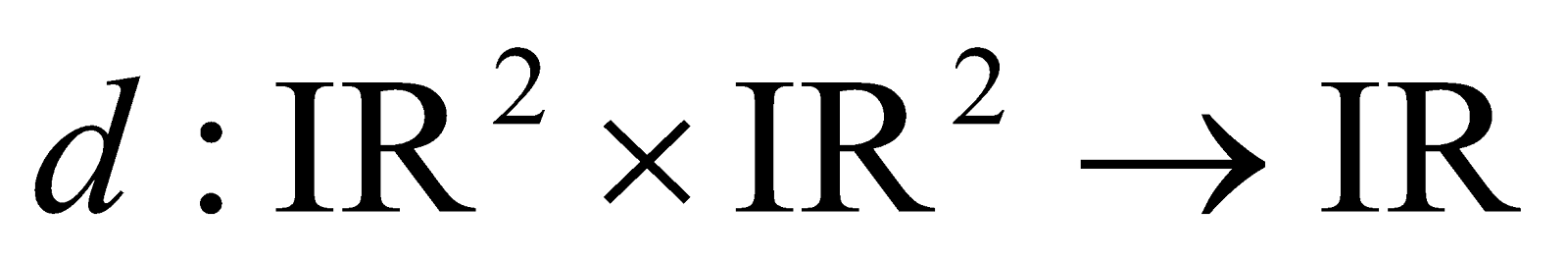 
defined by 
for all
, where
defined by for all, where 
. Show that 
is a metric on
3
(c) Let 
be a metric space and
. Show that 
(interior of
) is an open set. 2
be a metric space and. Show that (interior of) is an open set. 2
2. (a) Define a closed set. Show that in a metric spaceevery closed sphere in a closed set. 1+3=4
every closed sphere in a closed set. 1+3=4
(b) Prove that in a metric space any finite intersection of open sets is open. 4
any finite intersection of open sets is open. 4
Or
Letbe a metric space and. Then show thatis closed if and only ifcontains all its limit points.
be a metric space and. Then show thatis closed if and only ifcontains all its limit points.
(c) Define a product metric space. 1
3. (a) Define a convergent sequence in a metric space. 1
(b) Prove that in a metric space every convergent sequence has a unique limit. 3
(c) Show that the Euclidean space
is a complete metric space with the usual metric
defined by
is a complete metric space with the usual metricdefined by
Where
4
Or
Let
be a Cauchy sequence in a metric space. Prove thatis convergent if and only if it has a convergent subsequence.
be a Cauchy sequence in a metric space. Prove thatis convergent if and only if it has a convergent subsequence.
(d) Let
be a subspace of a metric space. Show that if 
is complete, and then 
is closed. 4
be a subspace of a metric space. Show that if is complete, and then is closed. 4
Or
Letbe a metric space and. Then show that
is dense in
if intersects every non-empty open set.
be a metric space and. Then show that is dense inif intersects every non-empty open set.
4. (a) Define a continuous function in a metric space. 1
(b) Letand
be metric spaces. Then prove that a function
is continuous if and only if
is closed in
, whenever 
is closed in 
. 4
andbe metric spaces. Then prove that a functionis continuous if and only ifis closed in, whenever is closed in . 4
(c) Letandbe metric spaces, be a continuous function and. Then show that the restriction 
is continuous on
. 3
andbe metric spaces, be a continuous function and. Then show that the restriction is continuous on. 3
Or
Let
and 
be two metric spaces and 
be a homeomorphism. Show that a subset 
is open if and only if its image 
is open.
and 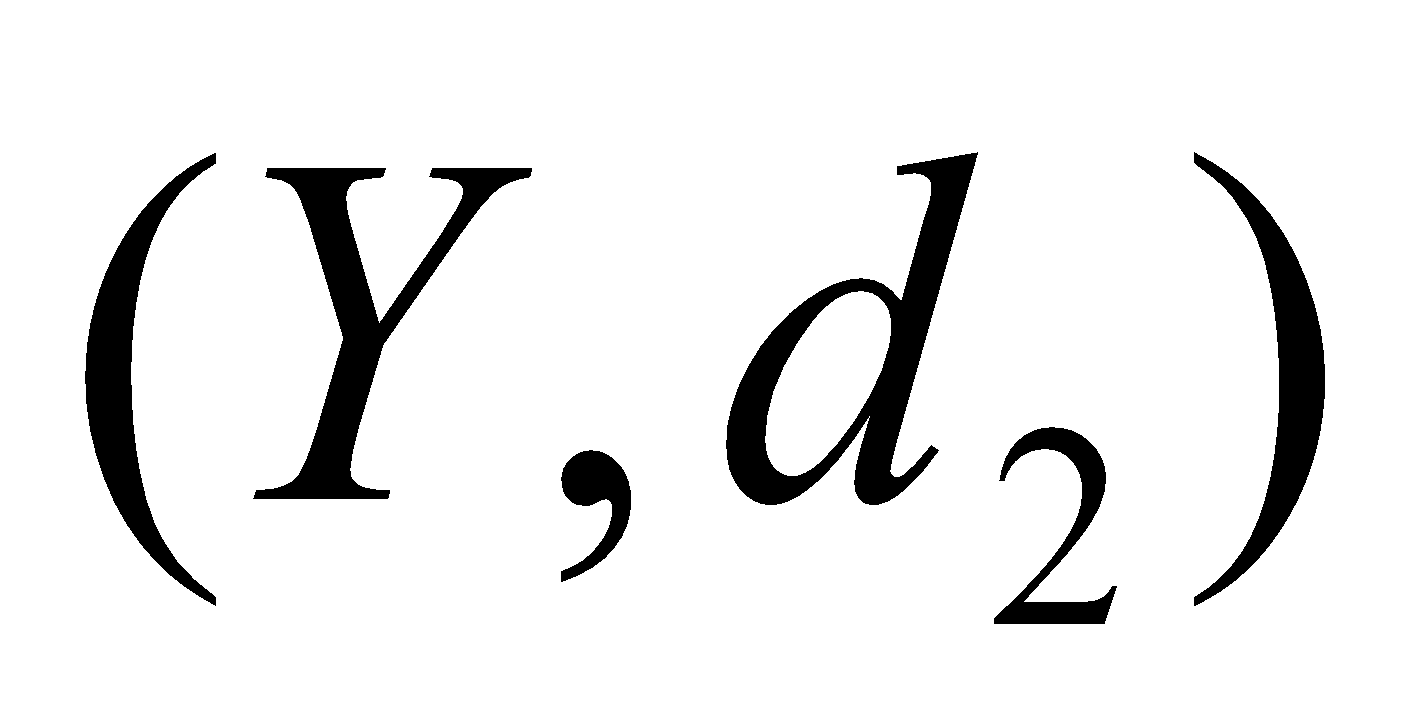be two metric spaces and be a homeomorphism. Show that a subset is open if and only if its image is open.
5. (a) Define a compact metric space. 2
(b) Show that a closed subset of a compact metric space is compact. 3
Or
Show that a compact metric space has Bolzano-Weierstrass property.
B: Statistics
(Marks: 40)
6. (a) What is empirical probability? Mention its relation with classical probability. 2
(b) Explain two merits of axiomatic probability. Define probability measure in terms of probability function. 2
(c) Two dice are rolled. Find the probability of getting ‘an even number on the first die or a total of 8’. 3
(d) The probability of A, B and C becoming officers in a firm were 
respectively. The probabilities that the bonus scheme will be introduced if A, B and C becomes officers are 
respectively. What is the probability that A will be officer if bonus scheme has been introduced? 4
respectively. The probabilities that the bonus scheme will be introduced if A, B and C becomes officers are respectively. What is the probability that A will be officer if bonus scheme has been introduced? 4
7. (a) What do you mean by dispersion? 1
(b) Find the mean and standard deviation for 542 numbers having class and frequency distribution as given below:
Class
|
20 – 30
|
30 – 40
|
40 – 50
|
50 – 60
|
60 – 70
|
70 – 80
|
80 – 90
|
Frequency
|
3
|
61
|
132
|
153
|
140
|
51
|
2
|
8. (a) Prove that correlation coefficient is independent of change of origin and scale. 3
(b) Calculating correlation coefficient between two variables 
and 
from, 25 pairs of observations obtained the following results:
and from, 25 pairs of observations obtained the following results: 
,
,
,
,
However, later on detected that actual pairs of values
8 12
6 8
Were considered as . Find the correct value of correlation coefficient. 4
. Find the correct value of correlation coefficient. 4
6 14
9 6
9. (a) Explain the nature of binomial distribution.
(b) Find 
for a binomial variate
, if 
and
. 2
for a binomial variate, if and. 2
(c) Mention the importance of Poisson distribution. Find the first two central moments of Poisson distribution. 4
(d) Find the expression for probability density function of the normal distribution with mean 
and unit variance. 5
and unit variance. 5
Or
Discuss about the chief characteristics of normal distribution and normal probability curve.
10. Discuss briefly the components of time series. Explain one of the methods used for measuring trend in time series. 6
Or
Find two monthly trend values of a factory for the month of November 2000 and September 2001 from the data given below by using principle of least squares:
Year
|
1996
|
1997
|
1998
|
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
Profit (in crores)
|
12.6
|
14.6
|
18.6
|
14.8
|
16.6
|
21.2
|
18.0
|
17.4
|
15.8
|
***
Post a Comment
Kindly give your valuable feedback to improve this website.