(A) Hydrodynamics
(Marks: 35)
1. (a) Define real and ideal fluid. 1
(b) Fill in the blank: 1
The motion of a fluid is said to be ____ when the vorticity of every fluid particle is zero.
2. (a) Given the velocity field
determine the acceleration of fluid particle of fixed identity. 2
(b) Deduce the equation of continuity in Cartesian coordinates. 6
3. Show that in a two-dimensional incompressible steady flow field the equation of continuity is satisfied with the velocity components in rectangular coordinates given by 5
where K is an arbitrary constant.
Or
Find the streamlines and paths of the particles when
4. (a) Write down the Euler’s equation of motion in vector form. 1
(b) Deduce the equation of motion under impulsive forces. 5
5. State and prove Kelvin’s circulation theorem. 6
Or
A sphere of radius R, whose centre is at rest, vibrates radially in an infinite incompressible fluid of density
, which is at rest at infinity. If the pressure at infinity is 
, show that the pressure at the surface of the sphere at time t is
, which is at rest at infinity. If the pressure at infinity is , show that the pressure at the surface of the sphere at time t is 
6. (a) Define flow and circulation. 2
(b) Show that there cannot be two different forms of irrotational motion for a given confined mass of liquids whose boundaries have prescribed velocities. 6
Or
A space is bounded by an ideal fixed surface 
drawn in a homogeneous incompressible fluid satisfying the conditions for the continued resistance of a velocity potential 
under conservative forces. Prove that the rate per unit time at which energy flows across into the space boundary by is
drawn in a homogeneous incompressible fluid satisfying the conditions for the continued resistance of a velocity potential under conservative forces. Prove that the rate per unit time at which energy flows across into the space boundary by is 
where 
is the density and 
an element of the normal to 
drawn into the space considered.
is the density and an element of the normal to drawn into the space considered.
(B) Hydrostatics
(Marks: 45)
7. (a) Define specific gravity and density of a fluid. 2
(b) Write True or False: 1
In a fluid, at rest under gravity, the pressure is the same at all points in the same horizontal plane.
8. Answer (a) and (b) or (c):
- Determine the necessary condition that must be satisfied by a given distribution of forces X, Y, Z; so that the fluid may maintain equilibrium.
- A small uniform tube is bent into the form of a circle whose plane is vertical. Equal quantities of two fluids of densities
and
fill half the tube. Show that the radius passing through the common surface makes with the vertical an angle
given by
Or
(c) (i) Prove that the surfaces of equal pressure are intersected orthogonally by the lines of force.
(ii) If a fluid is at rest under the forces X, Y, Z per unit mass, then find the differential equations of the curves of equal pressure and density. 3+4=7
9. (a) Define centre of pressure. 1
(b) State the principle of Archimedes in connection with a body immersed wholly or partially in a fluid. 2
10. (a) Find the centre of pressure of a parallelogram immersed in a homogeneous liquid with one side in the free surface. 6
Or
A circular area of radius 
is immersed with its plane vertical and centre at a depth
. Find the depth of centre of pressure.
is immersed with its plane vertical and centre at a depth. Find the depth of centre of pressure.
(b) Prove that the magnitude of the resultant thrust on a side of a plane surface immersed in a heavy homogeneous liquid (at rest under gravity) is given by the product of the area of the surface and the pressure at the centre of gravity of the area. 7
Or
A hollow cone is placed with its vertex upward on a horizontal table and liquid is poured in through a small hole in the vertex. If the cone begins to rise when the weight of the liquid poured in it equals its own weight, prove that its weight is to the weight of the liquid required to fill the cone is as
.
.
11. (a) State the conditions of equilibrium of a floating body. 2
(b) A rod of small cross-section and of density 
has a small portion of metal of weight 
that of the rod attached to one extremity. Prove that the rod will float at any inclination in a liquid of density 
if 
. 5
has a small portion of metal of weight 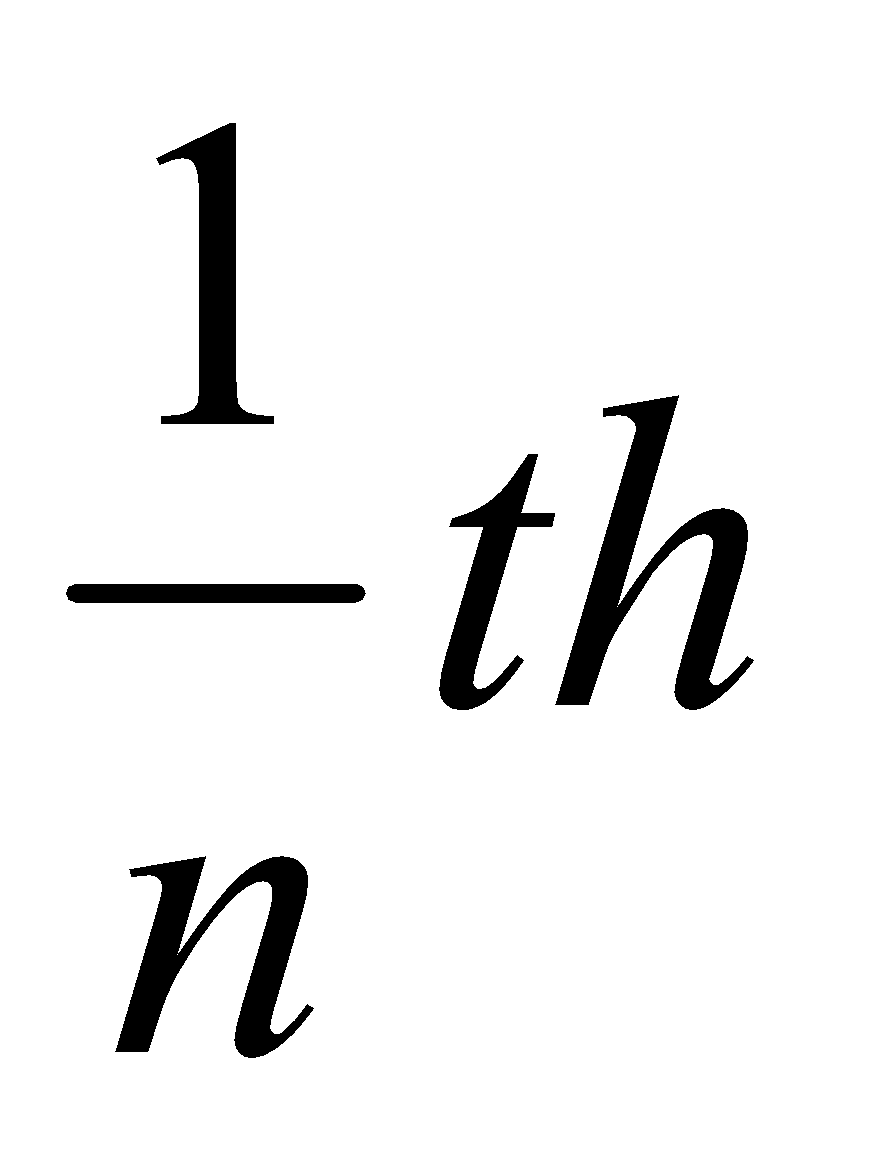that of the rod attached to one extremity. Prove that the rod will float at any inclination in a liquid of density if . 5Also Read: Dibrugarh University Question Papers
12. Show that the equilibrium is stable or unstable according as the met centre is above or below the centre of gravity of the body. 5
Or
A cylinder floating with its axis horizontal and in the surface is displaced in the vertical plane through the axis. Determine the position of meta centre.
***
Post a Comment
Kindly give your valuable feedback to improve this website.