[BA 2nd Sem Question Papers, Dibrugarh University, 2013, Mathematics, General, Matrices, Ordinary Differential Equations and Numerical Analysis]
2013 (May)
MATHEMATICS (General)
Course: 201
(Matrices, Ordinary Differential Equations and Numerical Analysis)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
GROUP – A
(Matrices)
1. (a) If
is a non-singular matrix of order
, what will be its rank? 1
is a non-singular matrix of order, what will be its rank? 1
(b) Find the rank by row transformations of the following: 3
(c) Find two non-singular matrices
and
such that
is in normal form, where 3
andsuch that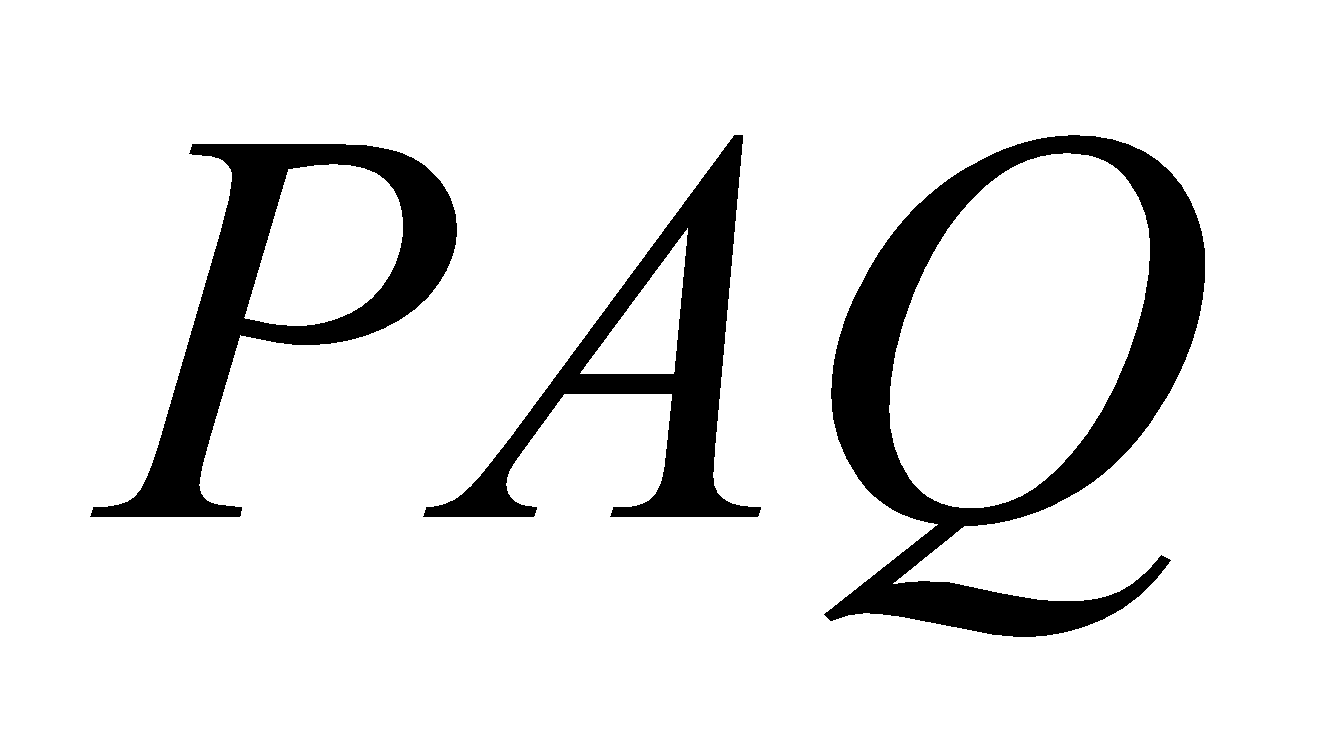is in normal form, where 3
2. (a) Define characteristic polynomial of square matrix.
(b) For what values of
the equations
the equations
are consistent?
(c) (Solve):
Or
Show that every spare matrix satisfies its characteristic equation.
(d) Determine the eigenvalues and eigenvectors: 4
GROUP – B
(Ordinary Differential Equations)
3. (a) Define an exact equation. 1
(b) Solve any one: 3
(c) Solve any one: 3
(d) Using Wronskian, examine whether the functions
are linearly independent or dependent.
are linearly independent or dependent.
4. (a) Solve any one: 5
(b) Solve any one: 5
(c) Solve any one: 5
5. (a) Answer any one: 5
- If
is a particular solution of
, find the general solution.
- Removing the first-order derivative, solve the following:
5
(b) Answer any one: 5
- Transform the equation
, where
are functions of
by changing the independent variable.
- Solve by changing the independent variable:
- Apply the method of variation of parameters to solve:
GROUP – C
(Numerical Analysis)
6. (a) Describe regula falsi method for solving an algebraic equation. 5
Or
Solve
for the root between
and
by bisection method.
for the root betweenandby bisection method.
(b) Describe Newton-Raphson method and interpret it geometrically. 5
Or
Find a real root of the following equation by iteration method: 
(c) Solve by Gauss-Jordan method: 5
7. (a) Deduce Newton’s backward interpolation formula. 5
Or
The population of a country was as follows:
 : |
1901
|
1911
|
1921
|
1931
|
1941
|
Population in (thousand):
|
46
|
66
|
81
|
93
|
101
|
Estimate the population for the year 1925, using Newton’s backward interpolation formula.
(b) Deduce Lagrange’s interpolation formula for unequal intervals. 5
Or
Given,
Find
,using Lagrange’s interpolation formula.
,using Lagrange’s interpolation formula.
Also Read: Dibrugarh University Question Papers
(c) Find the general quadrature formula for equidistant ordinates and deduce the trapezoidal rule. 3+2=5
Or
Find an approximate value of
by taking seven equidistant ordinates by using Simpson’s rule and trapezoidal rule.
by taking seven equidistant ordinates by using Simpson’s rule and trapezoidal rule.
***
Post a Comment
Kindly give your valuable feedback to improve this website.