[BA 3rd Sem Question Papers, Dibrugarh University, 2013, Mathematics, General, Group - A: Coordinate Geometry and Group -B: Analysis - (Real Analysis)]
GROUP – A
(Coordinate Geometry)
SECTION – I
(2- Dimension)
1. (a) Transform the equation
by changing to parallel axes of coordinates through the point
. 2
by changing to parallel axes of coordinates through the point. 2 (b) What will be the transformation of the equation 
when the two axes are turned through an angle
when the two axes are turned through an angleOr
To which point the origin will be shifted, so that the first degree terms in the equation
may be missed, when referred to the parallel displacement of the axes?
may be missed, when referred to the parallel displacement of the axes?2. (a) Find the angle between the two lines represented by the equation
(b) Determine the distance between the two parallel lines represented by the equation 3
Or
For what value of k the equation
(c) Show that the two straight lines represented by
are equally inclined to the straight line
. 3
are equally inclined to the straight line. 3 (d) Prove that the product of the lengths of perpendiculars drawn from the point
to the line 
is
to the line is
Or
Find the area of the triangle formed by the lines represented by
and axis of 
.
.3. (a) Reduce the equation 2
into standard form.
(b) Find the equation of the tangent drawn at the point 
to the conic 4
to the conic 4
Or
Show that the line 
will be a tangent to the conic 
if
will be a tangent to the conic if 
(c) Define Chord of contact, diameter and conjugate diameter. 2+1=3
Or
Determine the pole of the line 
with respect to the conic 
.
with respect to the conic .SECTION – II
(3-Dimension)
4. (a) Write the direction cosines of any normal to the plane 
.
. (b) Find the points of intersection of the plane 
with the coordinate axes.
with the coordinate axes. (c) What is the equation of the plane parallel to the plane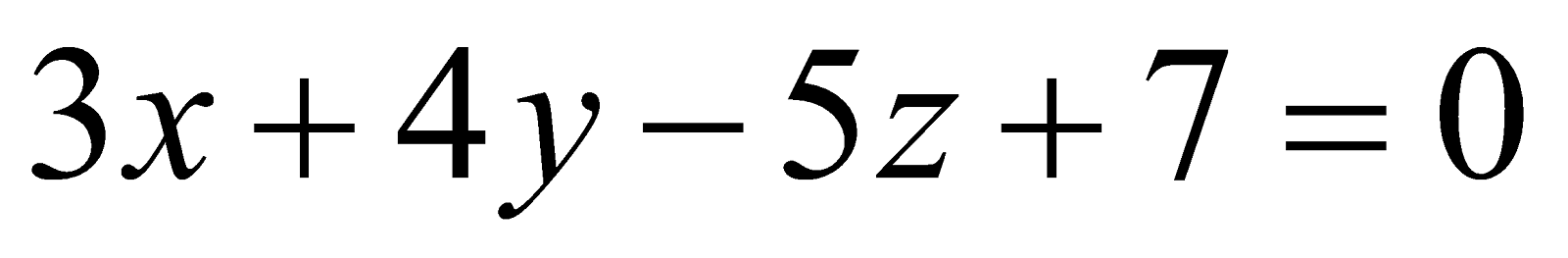
and passing through the origin?
and passing through the origin? (d) Find the equation of the plane passing through the point 
and perpendicular to each of the planes 
and
. 3
and perpendicular to each of the planes 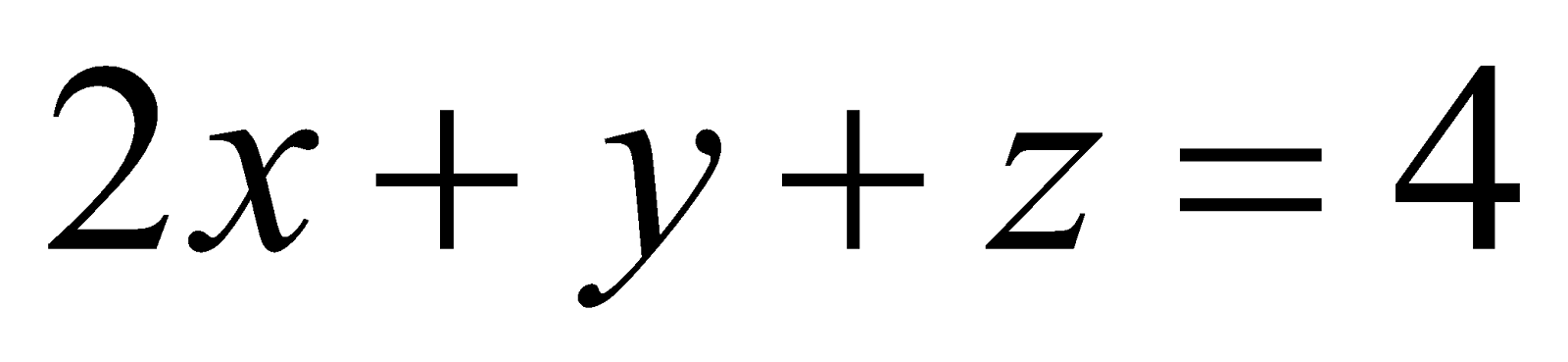and. 3Or
Find the locus of the point whose distance from the origin is three times its distance from the plane
.
. (e) Find the bisector of that angle between the planes 
and 
which contains the origin. 4
and which contains the origin. 4Or
Find the condition of representing two planes by the equation
.
.5. (a) Show that the two lines
are coplanar. Find the equation of the plane through the two lines.
Or
Prove that the plane through the line 
and perpendicular to the plane through the lines 
and 
and perpendicular to the plane through the lines and (b) Determine the shortest distance between the lines 
and the 
axis. 4
and the axis. 4Or
Find the equation of the line of shortest distance between the lines
GROUP – B
(Analysis – I)
6. (a) If 
, where n is a positive integer, show that 
. 2
, where n is a positive integer, show that . 2 (b) Find the radius of curvature of the parabola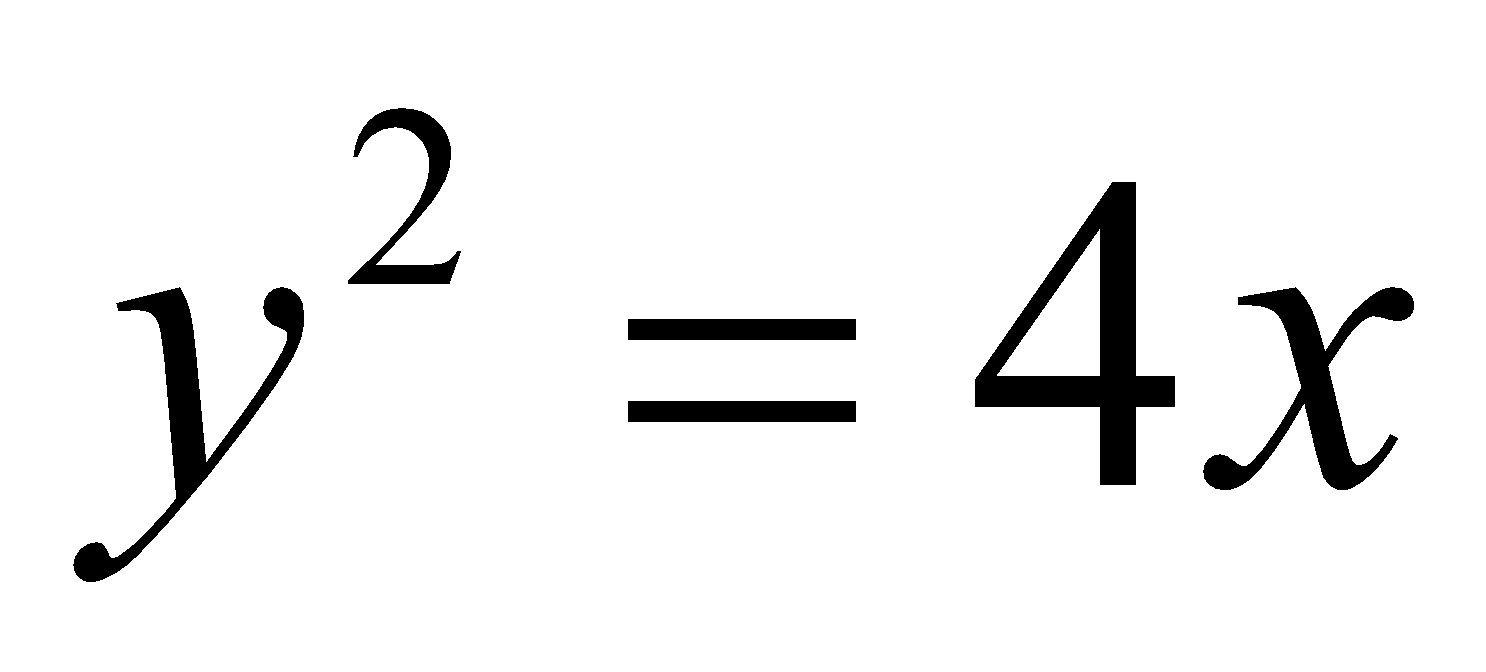 
at the vertex
. 2
at the vertex. 2 (c) Show that in any curve 2
(d) If 
show that
. 4
show that. 4Or
Evaluate: 2+2=4
7. (a) State Lagrange’s mean value theorem. 1
(b) Find the value of 
in Rolle’s Theorem where 
in 
2
in Rolle’s Theorem where in 2 (c) In the mean value theorem 
find c if 
and give a geometrical interpretation of the result. 3+1=4
find c if and give a geometrical interpretation of the result. 3+1=4Or
If 
find 
where 
and where
. 4
find where and where. 4 (d) Show that the function 
denied by
denied by 
Is continuous at
8. (a) State and prove Euler’s theorem on homogeneous function of two variables. 3
Or
If 
then show that
then show that 
(b) Show that 
if 
. 2
if . 29. (a) Prove that 
if 
3
if 3Or
Show that 
(b) If 
(m, n being positive integers), then deduce that 5
(m, n being positive integers), then deduce that 5
Or
Find the length of the arc of the parabola 
cut-off by its latus rectum.
cut-off by its latus rectum. Also Read: Dibrugarh University Question Papers
(c) Establish the reduction formula 2
where n is an integer.
***
Post a Comment
Kindly give your valuable feedback to improve this website.