[BA 3rd Sem Question Papers, Dibrugarh University, 2014, Mathematics, Major, Analysis - I (Real Analysis]
GROUP – A
(Differential Calculus)
(Marks: 35)
1. (a) If 
then write the value of 
1
then write the value of 1
(b) Find the limit: 2
(c) Define sub tangent. Show that the sub tangent at any point of a parabola varies as the abscissa of the point of contact. 1+2=3
(d) If 
then prove that 
then prove that
Or
Show that the radius of curvature at the origin of the conic 
is 
is
2. (a) Give an example of a continous function in a domain which has neither infimum nor supremum therein.
(b) If a function 
satisfies the conditions of Lagrange’s mean value theorem and also 
then show that is constant on
.
satisfies the conditions of Lagrange’s mean value theorem and also then show that is constant on.
(c) If 
then prove that
then prove that 
Or
Using Maclaurin’s theorem, expand 
in an infinite series.
in an infinite series.
(d) Discuss the applicability of the Rolle’s Theorem for 
in
.
in.
3. (a) Define homogeneous function of two variables. 1
(b) If 
then show that 4
then show that 4
Or
If u is a homogeneous function, of degree n, of x and y, then show that
4. (a) State Young’s theorem. 1
(b) If 
then show that 4
then show that 4
(c) If 
and 
are twice differentiable functions and 
then prove that 5
and are twice differentiable functions and then prove that 5
c is a constant.
Or
Find the extreme values of 
GROUP – B
(Integral Calculus)
(Marks: 20)
5. (a) Write the reduction formula for 1
(b) Prove that 2
(c) Show that 4
(d) Evaluate:
Or
Prove that
6. (a) If 
and 
be the vectorial angles of A and B respectively, then write the formula for arc 
1
and be the vectorial angles of A and B respectively, then write the formula for arc 1
(b) Find the perimeter of the cardioids
5
5
(c) Find the area of the surface of revolution formed by revolving the curve 
about the initial line. 4
about the initial line. 4
Or
Find the volume of the solid generated by revolving the asteroid
about the x-axis.
GROUP – C
(Riemann Integral)
(Marks: 25)
7. (a) Define refinement of a partition. 1
(b) Show that the function 
defined by
defined by 
is not integrable on any interval. 2
(c) Prove that every continuous function is Riemann integrable. 5
Or
If 
when
)
when)
, when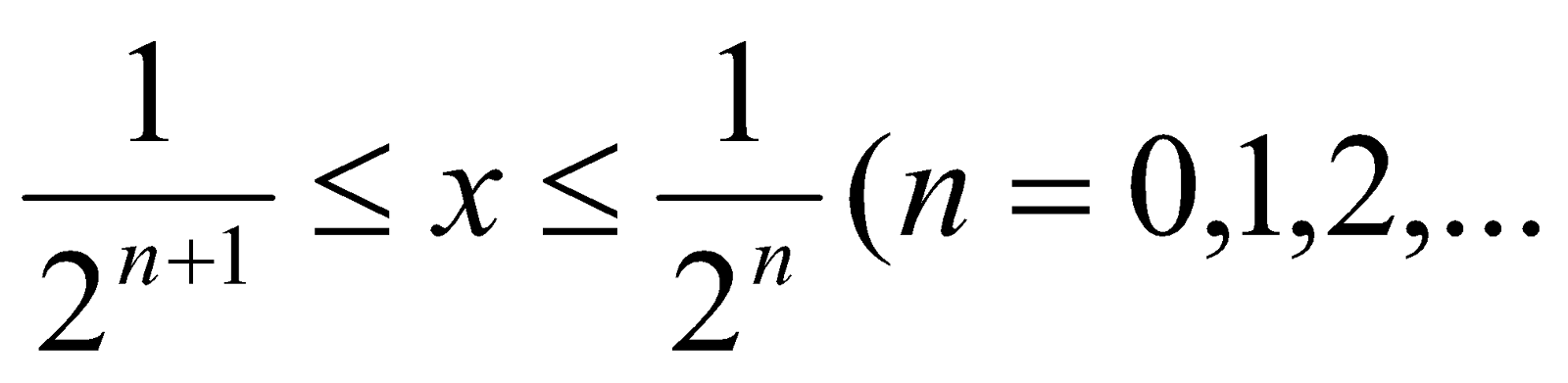 
then show that 
although it has many points of discontinuity.
although it has many points of discontinuity.
8. (a) State the fundamental theorem of integral calculus. 1
(b) If 
is a continuous function on
, then show that there exists a number 
such that 
3
is a continuous function on, then show that there exists a number such that 3
(c) If a function is bounded and integrable on, then the function F defined as
is bounded and integrable on, then the function F defined as 
Is continuous on. Prove it. 3
. Prove it. 3
Or
Verify the mean value theorem for 
in the interval
.
in the interval.
9. (a) State the Dirichlet test for convergence of integral of a product. 1
(b) Test for convergence of 2
(c) Prove that 
is convergent for 
3
is convergent for 3Also Read: Dibrugarh University Question Papers
10. Answer any one of the following: 4
(a) Prove that 
(b) Prove that 
***
Post a Comment
Kindly give your valuable feedback to improve this website.