[BA 2nd Sem Question Papers, Dibrugarh University, 2014, Mathematics, General, Matrices, Ordinary Differential Equations and Numerical Analysis]
2014 (May)
MATHEMATICS (General)
Course: 201
(Matrices, Ordinary Differential Equations and Numerical Analysis)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
1. (a) Define elementary matrix. 1
(b) Find the rank of the following matrix by reducing it to normal form: 4
(c) Show that 3
rank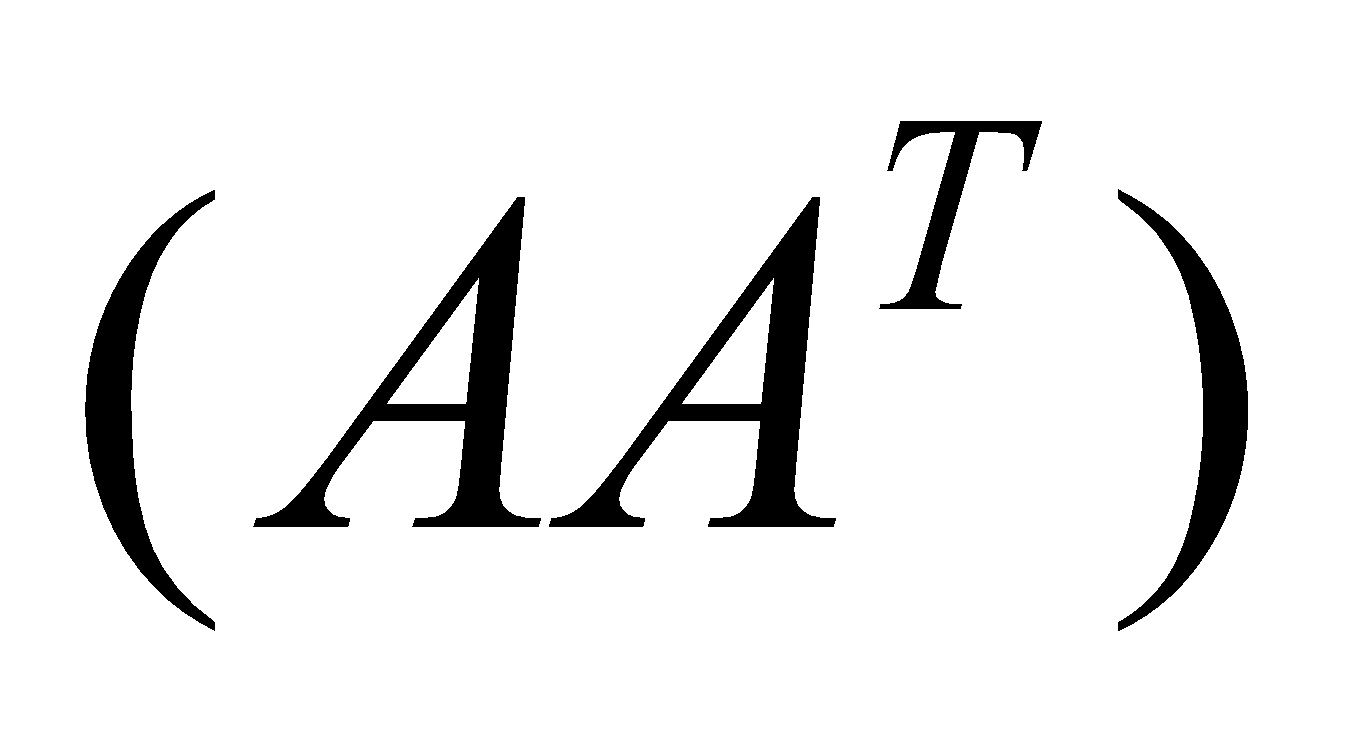
= rank
= rank
2. (a) Show that the following equations are consistent and solve them: 3
(b) Define characteristic roots and characteristic vectors of a square matrix. 1+1=2
(c) Verity Cayley-Hamilton theorem for the following matrix: 5
Or
Show that the inverse of a non-singular matrix can be computed with the help of the Cayley-Hamilton theorem.
GROUP – B
(Ordinary Differential Equations)
(Marks: 30)
3. (a) Write the standard form of linear equation of first-order differential equation. 1
(b) Solve any one: 3
(c) Solve any one: 3
(d) Prove that
and
are solutions of the differential equation
and these solutions are linearly independent. 3
andare solutions of the differential equationand these solutions are linearly independent. 3
4. (a) Solve any two: 3x2=6
(b) Solve any one: 4
5. (a) Removing the first-order derivative, solve the following equation: 5
Or
Solve by changing the independent variable:
(b) Apply the method of variation of parameters to solve the equation. 5
, where
,
and
are functions of
.
Or
If
is a particular solution of
is a particular solution of 
GROUP – C
(Numerical Analysis)
(Marks: 30)
6. (a) Write the condition of convergence of Newton-Raphson method. 1
(b) Describe bisection method for solving an algebraic equation. 4
Or
Find one root of the following equation by iterative method:
(c) Apply Newton-Raphson method to find the cube root of 25. 5
Or
Find the real root of the equation, 
by regula falsi method, correct to three places of decimal.
by regula falsi method, correct to three places of decimal.
(d) Describe the solution of system of linear equations by Gauss elimination method. 5
Or
Solve by Gauss-Jordan method:
7. (a) Show that
2
2
(b) Deduce Newton’s forward interpolation formula. 5
Or
Given
 : |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
 : |
1
|
8
|
27
|
64
|
125
|
216
|
343
|
512
|
Then find 
(c) Obtain the value of
by using trapezoidal rule from the relation: 5
by using trapezoidal rule from the relation: 5
Or
Given
| : |
1
|
3
|
4
|
6
|
10
|
| : |
0
|
18
|
48
|
180
|
900
|
Then find the value of
by using Lagrange’s interpolation formula.
by using Lagrange’s interpolation formula. Also Read: Dibrugarh University Question Papers
(d) Deduce Simpson’s
rule. 3
rule. 3
***
Post a Comment
Kindly give your valuable feedback to improve this website.