[BA 3rd Sem Question Papers, Dibrugarh University, 2014, Mathematics, Major, Coordinate Geometry and Algebra - I]
GROUP – A
(Coordinate Geometry)
SECTION – I
(2-Dimension)
(Marks: 27)
1. (a) Find out the angle between the pair of lines represented by the equation
1
(b) Choose a new origin (h, k), without changing the directions of the axes such that the equation
may reduce to the form 
2
2
(c) Transform the equation
To rectangular axes inclined at angle 
to the old rectangular axes. 3
to the old rectangular axes. 3
Or
Find the angle through which the axes be rotated so that the expression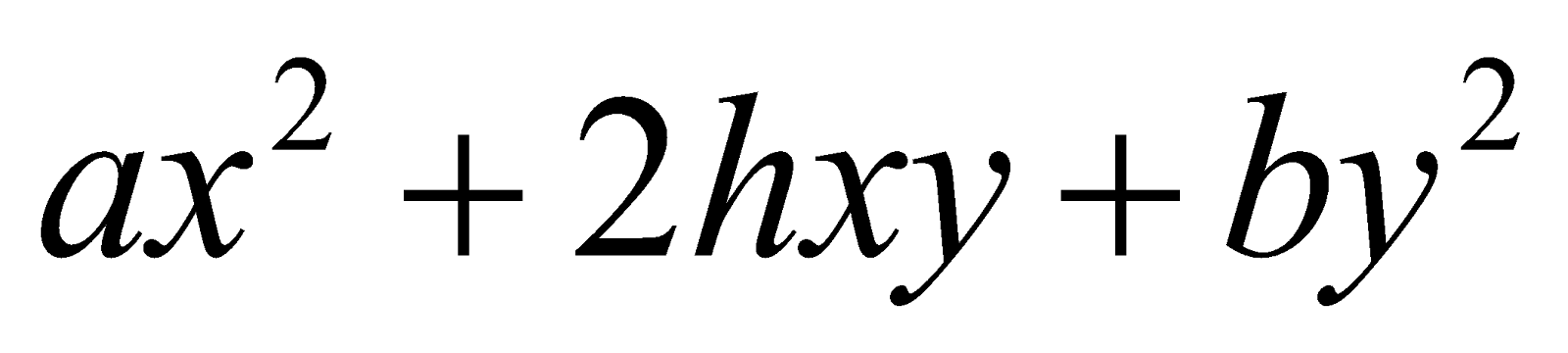 
may become of the form 
may become of the form
2. (a) Find the value of 
so that the equation 3
so that the equation 3
may represent a pair of lines.
(b) Find the equation of the pair of lines through the origin which represents the lines perpendicular to the pair of lines
. 3
. 3
Or
Show that the angle between one of the lines given byand one of the lines 
is equal to the angle between the other two lines of the systems.
and one of the lines is equal to the angle between the other two lines of the systems.
(c) Prove that the straight lines represented by the equation
Will be equidistant from the origin if
5
Or
If represents a pair of lines, prove that the area of the triangle formed by these lines and the x-axis is
represents a pair of lines, prove that the area of the triangle formed by these lines and the x-axis is 
3. (a) State True or False: 1
When the focus lies on the directrix, the conic section is a pair of lines.
(b) Find the equation of the chord of contact of tangents from a point 
to the conic 4
to the conic 4
Or
Find the condition that the pair of lines 
may be conjugate diameters of the conic
may be conjugate diameters of the conic 
(c) Reduce the following equation to the standard form:
5
Or
Prove that every Cartesian equation of the second degree, i.e.
represents a conic.
SECTION – II
(3-Dimension)
(Marks: 18)
4. (a) Write the direction cosines of the line joining the origin and the point 
. 1
. 1
(b) Find the equation of the plane which passes through the intersection of the planes 
and is perpendicular to the plane 
4
and is perpendicular to the plane 4
(c) Find the distance of the point 
from the plane 
measured parallel to the line
from the plane measured parallel to the line 
5
Or
Show that the lines
and 
intersect. Find the coordinates of the point of intersection.
5. (a) What is the shortest distance between two intersecting straight lines? 1
(b) Find the shortest distance between the line
2
and the z-axis.
(c) Find the length and the equations of the shortest distance between the lines
5
Or
Prove that the shortest distance between the lines
is 
and the equation of shortest distance are
and the equation of shortest distance are 
GROUP – B
(Algebra – I)
(Marks: 35)
6. (a) If a set A has n members, then state the number of binary compositions on A. 1
(b) The set of integers, with respect to usual multiplication does not form a group. Justify it. 2
(c) State True or False: A group of prime order is Abelian. 1
(d) Answer any two questions: 3x2=6
- Show that the centre of a group G is a subgroup of G.
- If G is a group is which
for three consecutive integers
and any a, b in G, then show that G is Abelian.
- Prove that an infinite cyclic group has precisely two generators.
7. Answer any two questions: 5x2=10
- Let G be a group. Suppose
such that –
.
- If H and K are finite subgroups of a group G, then prove that
- If a group has finite number of subgroups, then show that it is a finite group.
8. (a) Define Kernel of a group homomorphism. 1
(b) Prove that a subgroup H of a group G is normal in G iff 
for all 
4
for all 4Also Read: Dibrugarh University Question Papers
9. Answer any two questions: 5x2=10
- If G is a group such that
is cyclic, where
is centre of G, then show that G is Abelian?
- Prove that every quotient group of a cyclic group is cyclic.
- State and prove fundamental theorem of group homomorphism.
***
Post a Comment
Kindly give your valuable feedback to improve this website.