[BA 1st Sem Question Papers, Dibrugarh University, 2013, Mathematics, Major]
1. (a) Choose the correct answer for the following: 1
A sequence is bounded if and only if
- Its domain is bounded.
- Its range is bounded.
- It is bounded above.
- It is bounded below.
(b) Write the bounds of the sequence 
where
where 
(c) Write the bounds of the sequence 
where
where 
Is a bounded sequence
(d) Show that a sequence converges to one limit point only.
Or
Show that every bounded sequence with a unique limit point is convergent.
2. (a) Write when an infinite series diverges.
(b) Write the statement of Leibnitz test for convergence of an alternating series.
(c) Test the convergence of the infinite series
.
.
(d) Test the convergence of the infinite series 
(e) Show that if a series 
of positive monotonic decreasing terms converges, then 
as 
.
of positive monotonic decreasing terms converges, then as .
Or
Test the convergence of the infinite series
.
.
3. (a) If 
be a root of an equation 
, then write a factor of 
. 1
be a root of an equation , then write a factor of . 1
(b) If 
and 
are two roots of the equation
, then write the other two roots of the equation. 1
and are two roots of the equation, then write the other two roots of the equation. 1
(c) Write the nature of the roots of the equation 
2
2
(d) If 
are the roots of the equation 
then write the equation whose roots are 
2
are the roots of the equation then write the equation whose roots are 2
(e) If 
be the roots of the equation 
then find the value of
be the roots of the equation then find the value of 
3
(f) Solve the equation 
by Cardan’s method. 6
by Cardan’s method. 6
Or
If 
be the roots of the equation 
then find the value of 
.
be the roots of the equation then find the value of .
GROUP – B
(Trigonometry)
4. (a) Choose the correct answer:
is equal to 
(b) Write the roots of the quadratic equation 
(c) Express 
in powers of 
.
in powers of .
Or
If 
prove that 
prove that
5. (a) Show that 
2
2
(b) Show that 
3
3
Or
Express 
in the form 
in the form
6. (a) Write the interval of x for which 
1
(b) Show that
3
Or
Expand 
in ascending powers of 
in ascending powers of
7. (a) Choose the correct answer: 1
is equal to 
(b) Write the period of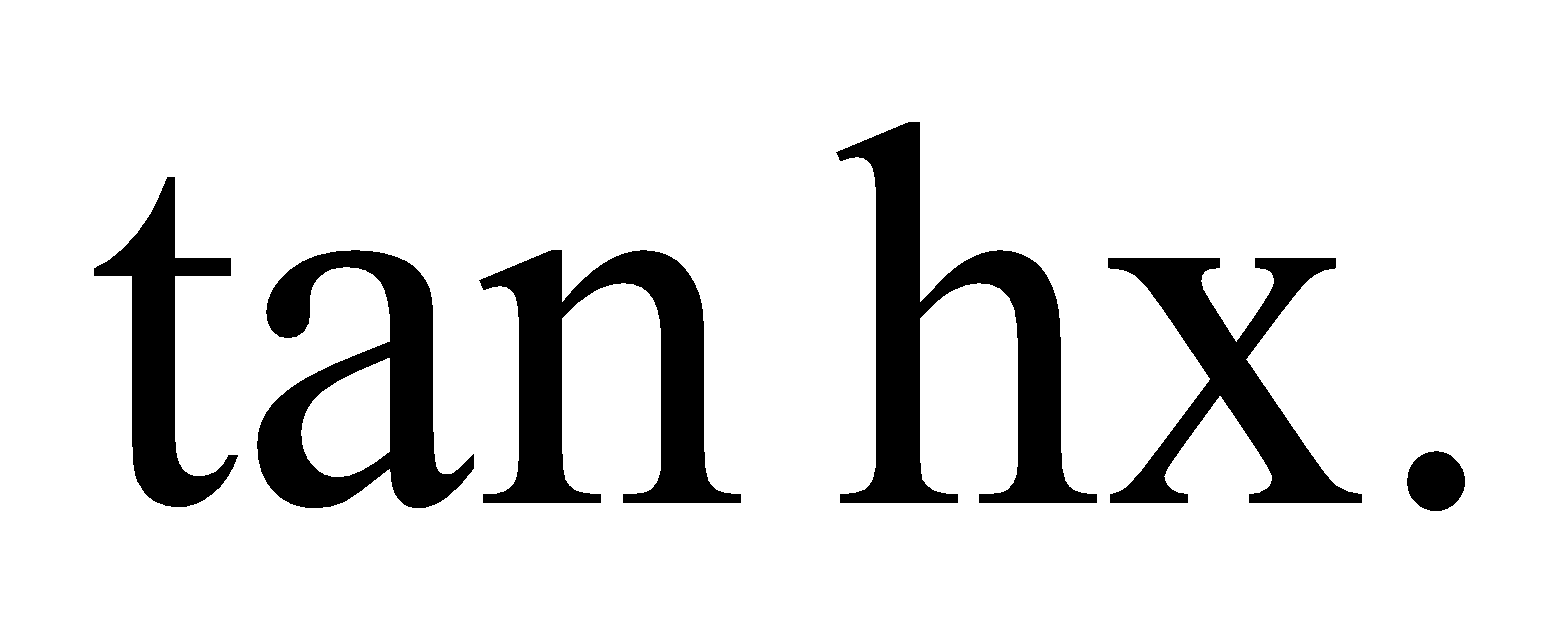 
1
1
(c) Write the expansion of 
in terms of x. 2
in terms of x. 2
(d) Find the sum of 
up to 
terms. 4
up to terms. 4
Or
Separate 
into real and imaginary parts.
into real and imaginary parts.
GROUP – C
(Vector Calculus)
8. (a) Choose the correct answer: 1
A vector 
is a solenoidal vector of
is a solenoidal vector of 
(b) Find
, where 
2
, where 2
(c) Show that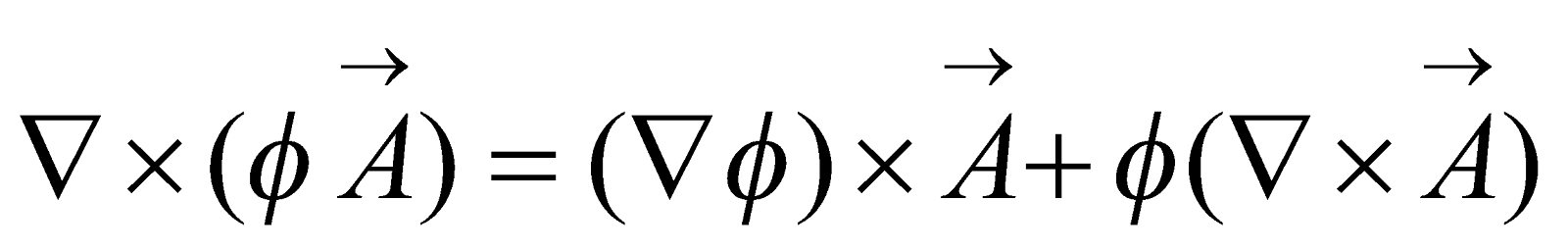
, where 
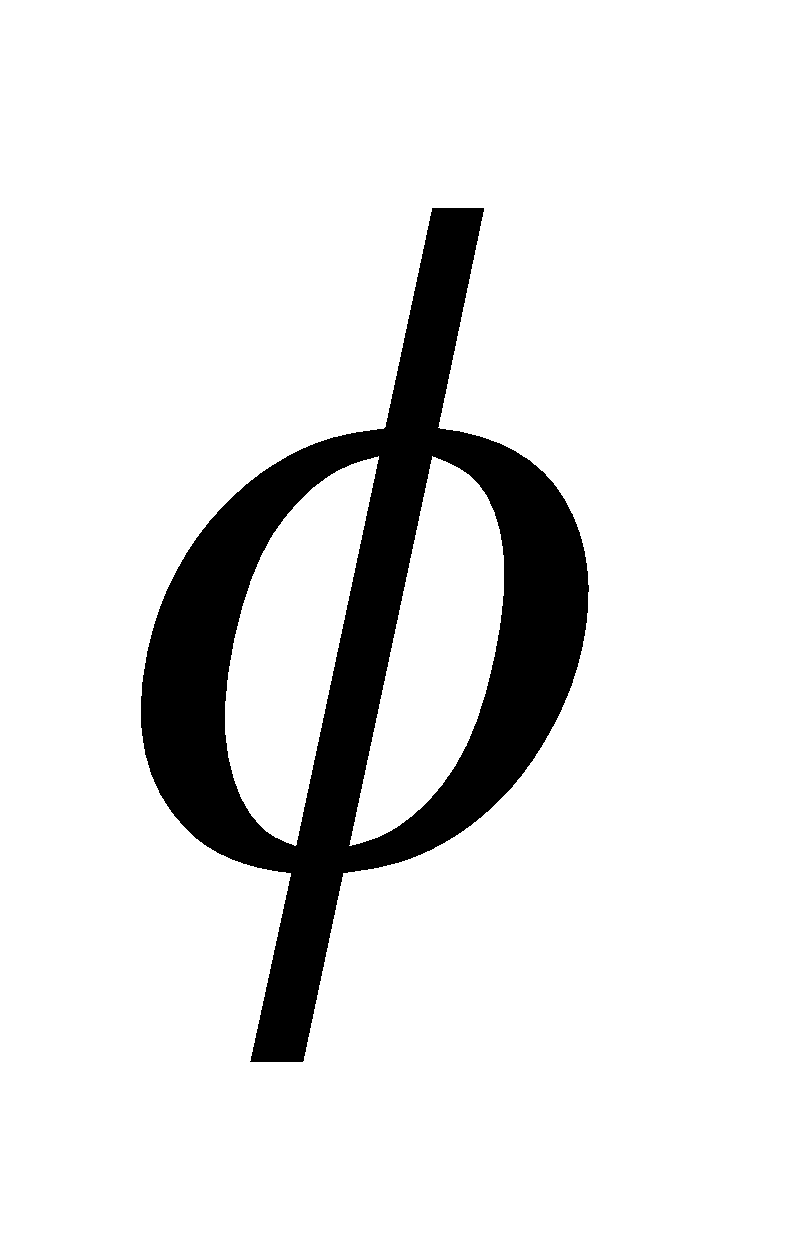is a scalar function and 
is a vector function. 5
, where is a scalar function and is a vector function. 5
Or
Show that 
where 
where
(d) Show that 
is a vector perpendicular to the surface 
where 
is a constant. 3
is a vector perpendicular to the surface where is a constant. 3
(e) Evaluate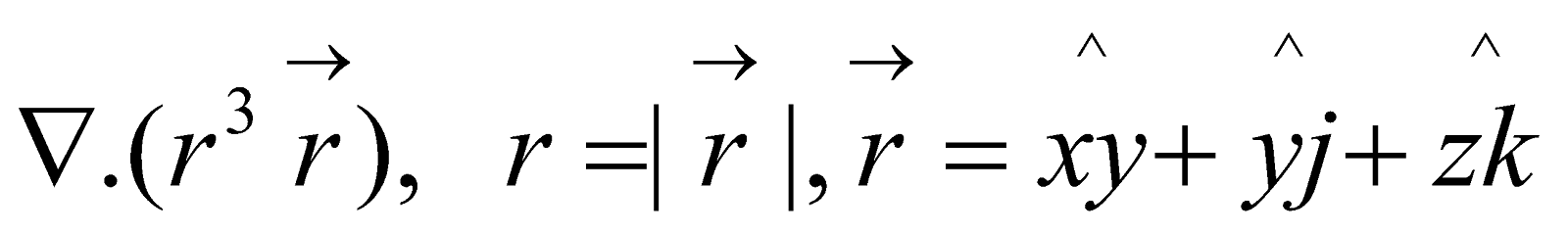 
4
4
Or
Find the directional derivative of 
in the direction of 
in the direction of
***
Post a Comment
Kindly give your valuable feedback to improve this website.