[BA 4th Sem Question Papers, Dibrugarh University, 2014, Economics, Major, Mathematics for Economics]
1. Choose the correct answer: 1x8=8
is
- Given
- In the determinant
, the minor of element 8 is
- 0
- 8
- – 3
- – 6
- Given the
function
the
function is
- Rank of the matrix
is
- 1
- 2
- 3
- 4
- The function
is not continuous at
- 1
- 2
- 3
- None of the above
2. Answer any four of the following: 4x4=16
- Find the numbers a and b that make A the inverse of B, when
- Illustrate Hawkins-Simon conditions.
- Draw the graph of
- Derive the elasticity of substitution for Cobb-Douglas production function.
- Evaluate:
- Given the input coefficient matrix
Explain the economic meaning of the third column sum and the third row sum.
3. (a) (i) Define the following with examples: 1x4=4
Null set; Disjoint set; Convex set; Union of sets.
(ii) Define limit of a function.
(iii) A function is given by
find whether the function is continous at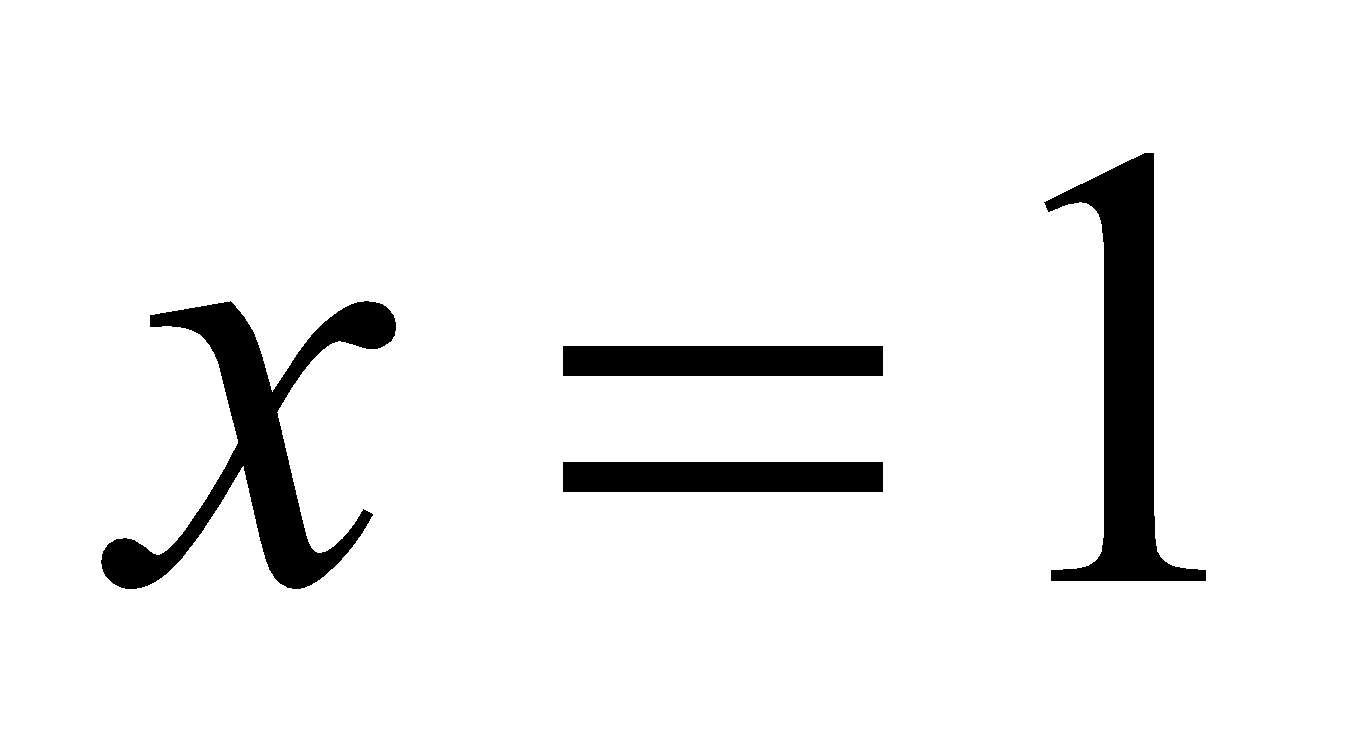
or not. 4
or not. 4Or
(b) (i) If
,
; find 
3
,; find 3 (ii) Solve the following pair of equations graphically: 5
(iii) Define continuity of a function. 3
4. (a) (i) Consider the following macro-economic model of two countries, 
that trade with each other:
that trade with each other: 
Here
is income, 
is consumption, 
is (exogenous) autonomous expenditure, 
denotes exports and
denotes imports of country 
. Find the equilibrium values of 
and 
by matrix algebra. 7
is income, is consumption, is (exogenous) autonomous expenditure, denotes exports anddenotes imports of country . Find the equilibrium values of and by matrix algebra. 7 (ii) Distinguish between the following: 2+10=12
(a) Static and Dynamic input-output models.
(b) Open and Closed input-output models.
Or
(b) (i) Verify that the following Matrix A is idempotent: 10+2=12
(ii) Given the technical coefficient matrix (A) and the final demand vector (F), find the consistent level of sectoral output in a static input-output framework:
5. (a) Distinguish between Cobb-Douglas production function and CES production function. State and prove the properties of CES production function. 2+10=12
Or
(b) (i) A consumer has a utility function
. Does the utility function display diminishing marginal utility? 5
. Does the utility function display diminishing marginal utility? 5 (ii) Find out
, when
3
, when 3 (iii) The AR function is given by
function is given by
. Find the elasticity of demand at
. 4
function is given by. Find the elasticity of demand at. 46. (a) (i) Find 
5
5 (ii) Given the MC function
, find the level of output
at which the
will be minimum. 6
, find the level of outputat which thewill be minimum. 6Or
(b) (i) Given the marginal propensity to import
and the information that
when
, find the import function
. 4
and the information thatwhen, find the import function. 4 (iii) Define consumer’s surplus. Given the demand function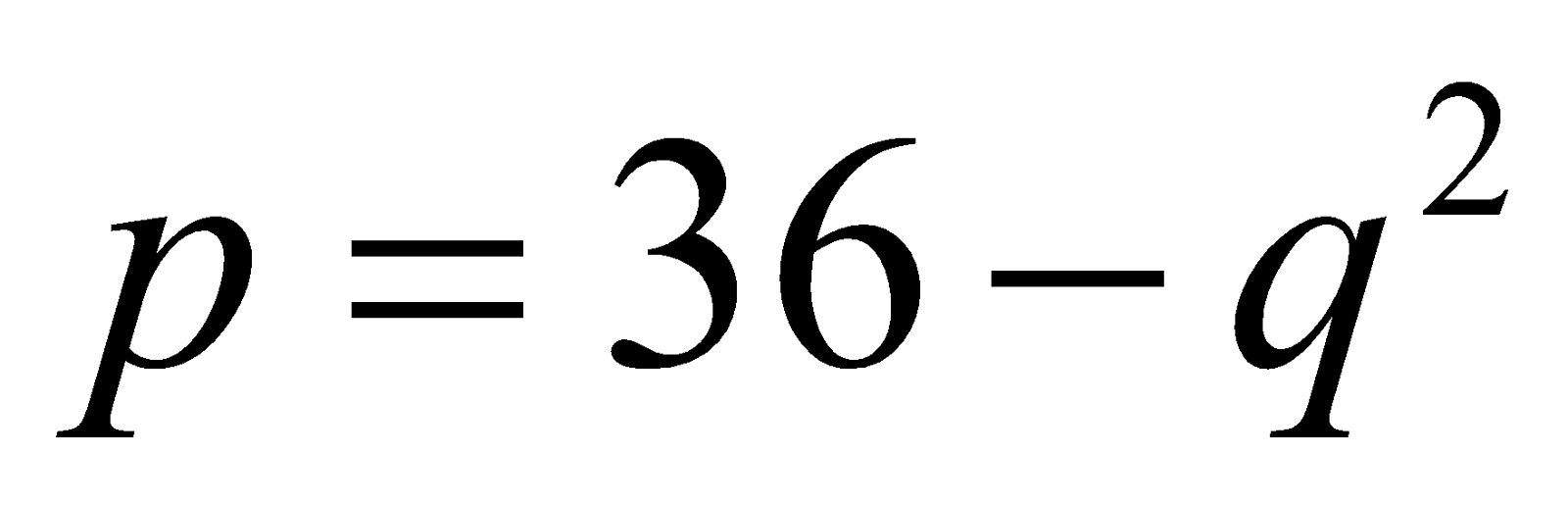
and the supply function
, find the consumer’s surplus at equilibrium. 2+10=12
and the supply function, find the consumer’s surplus at equilibrium. 2+10=12Also Read: Dibrugarh University Question Papers
7. (a) (i) Let the demand and supply functions be
, 
10+2=12
, 10+2=12
Assuming that the rate of change of price over time is directly proportional to the excess demand, find the time path
.
. (ii) Briefly explain the use of differential equations in economics.
(b) (i) In a market model
and 
. Find the time path
and test whether the time path is convergent.
. Find the time pathand test whether the time path is convergent. (ii) Write a note on the cobweb model.
***
Post a Comment
Kindly give your valuable feedback to improve this website.