[BA 3rd Sem Question Papers, Dibrugarh University, 2013, Mathematics, Major, Analysis - I (Real Analysis]
GROUP – A
(Differential Calculus)
(Marks: 35)
1. (a) If  then write the value of
then write the value of  is the positive integer. 1
is the positive integer. 1
(b) Find the value of 2
(c) Show that the subnormal at any point of a parabola is of constant length. 3
Or
Find the curvature of the ellipse  and
and  at
at 
(d) If  then show that 4
then show that 4
Or
If  is the angle between the radius vector and the tangent at any point of the curve
is the angle between the radius vector and the tangent at any point of the curve  then prove that
then prove that 
2. (a) State Darboux’s theorem in differential calculus. 1
(b) If a function  is continuous in
is continuous in  and differentiable in
and differentiable in  such that
such that  then prove that
then prove that  is strictly increasing on
is strictly increasing on . 2
. 2
(c) State and prove Cauchy’s mean value theorem. 3
Of
If  is continuous on
is continuous on  and differentiable in
and differentiable in  and
and  then show that
then show that
(d) Prove that  4
4
Or
Expand  in powers of
in powers of  for
for 
3. (a) State and Euler’s theorem on homogeneous function of two variables. 1
(b) If  then prove that
then prove that  4
4
Or
If  , then prove that
, then prove that
4. (a) State Schwarz’s theorem. 1
(b) If  then show that 2
then show that 2
(c) If  then prove that
then prove that  3
3
(d) Prove that  has neither maximum nor minimum at
has neither maximum nor minimum at  4
4
Or
If  , where
, where  , then prove that
, then prove that
GROUP – B
(Integral Calculus)
(Marks: 20)
5. (a) If  then write the relation between
then write the relation between  and
and  1
1
(b) Show that  2
2
(c) Evaluate:  3
3
(d) Deduce the reduction formula for  4
4
Or
Prove that 
6. (a) If  then write the length of arc
then write the length of arc  where A and B have abscissa a and b respectively. 1
where A and B have abscissa a and b respectively. 1
(b) Find the whole length of the curve  5
5
Or
Find the volume of the solid generated by revolving the ellipse  about the major axis.
about the major axis.
(c) Find the surface of the solid formed by revolving the cardioids  about the initial line. 4
about the initial line. 4
GROUP – C
(Riemann Integral)
(Marks: 25)
7. (a) What is the essential condition for a function  to be Riemann integrable in [a, b]? 1
to be Riemann integrable in [a, b]? 1
(b) Prove that for any two partitions  and
and  of
of
 . 2
. 2
(c) Show that every monotonic function on  is Riemann integrable. 5
is Riemann integrable. 5
Or
If  and
and 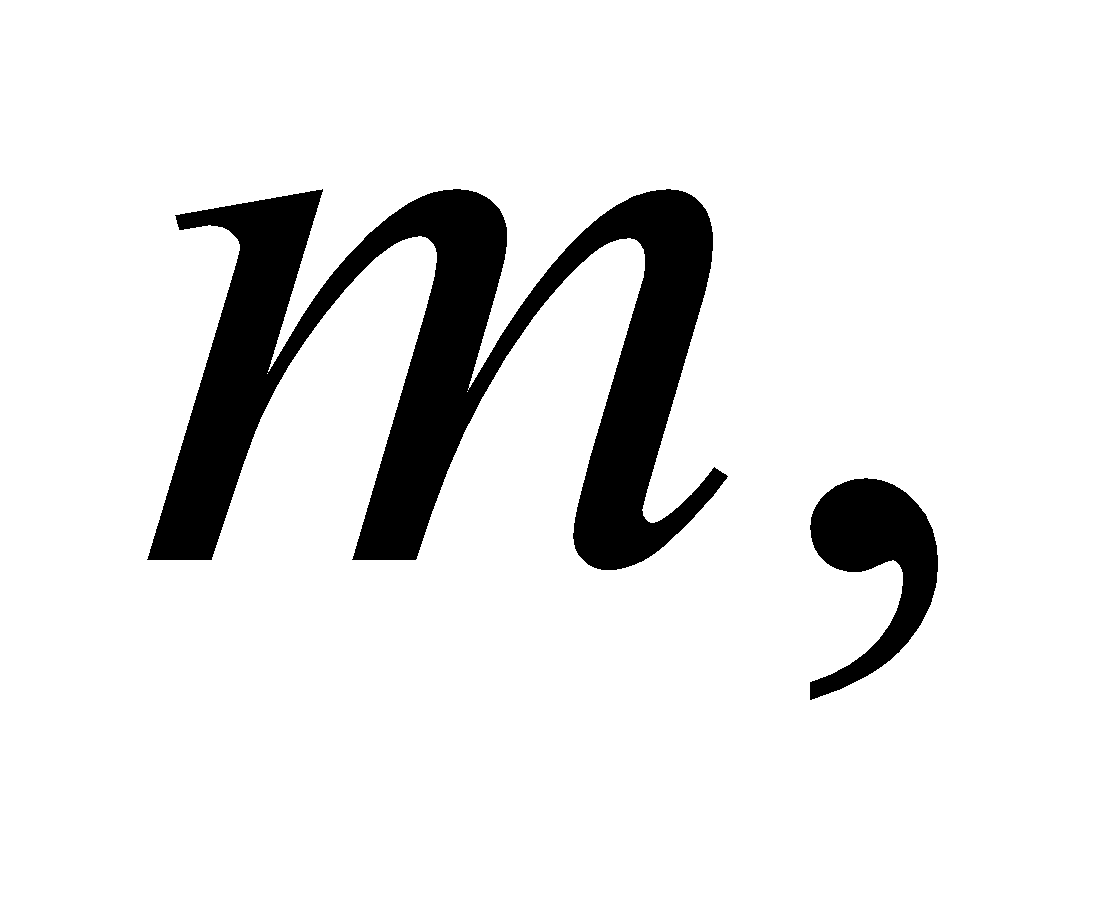
 are lower and upper bounds of
are lower and upper bounds of  on
on , then show that
, then show that
8. (a) State first mean value theorem of integral calculus. 1
(b) A function having primitive may not be continuous. Justify it. 3
(c) If  and g are integrable on
and g are integrable on  and
and keeps the same sign over
keeps the same sign over  , then show that
, then show that  and
and  where m, M are bounds of g on
where m, M are bounds of g on  . 3
. 3
9. (a) Define Abel’s test for convergence of integral of a product. 1
(b) Show that
Converges to 0 2
(c) Test for convergence (any one): 3
Also Read: Dibrugarh University Question Papers
10. (a) Prove that 4
(b) Prove that
***


Post a Comment
Kindly give your valuable feedback to improve this website.