[BA 3rd Sem Question Papers, Dibrugarh University, 2015, Mathematics, Major, Analysis - I (Real Analysis)]
GROUP – A
(Differential Calculus)
(Marks: 35)
1. (a) If  then write the value of
then write the value of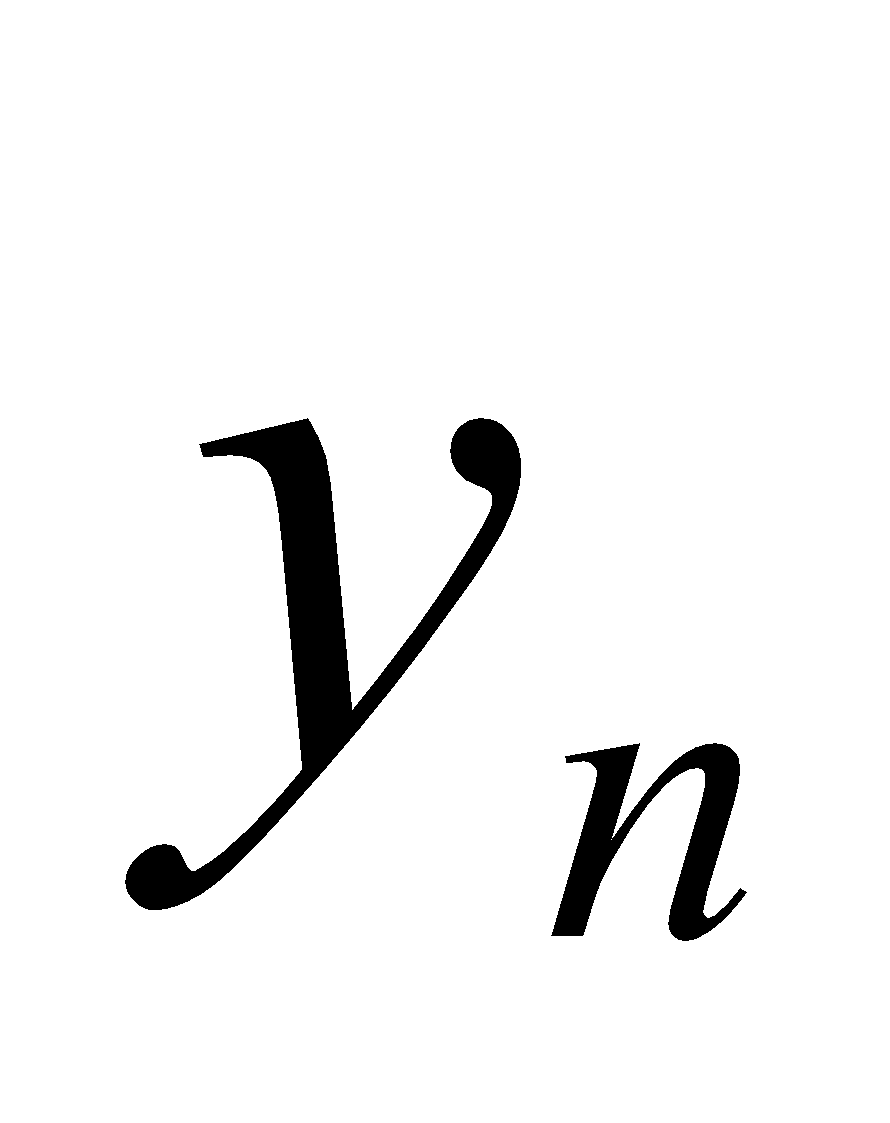 . 1
. 1
(b) Evaluate: 2
(c) Find the length of the subnormal to the curve 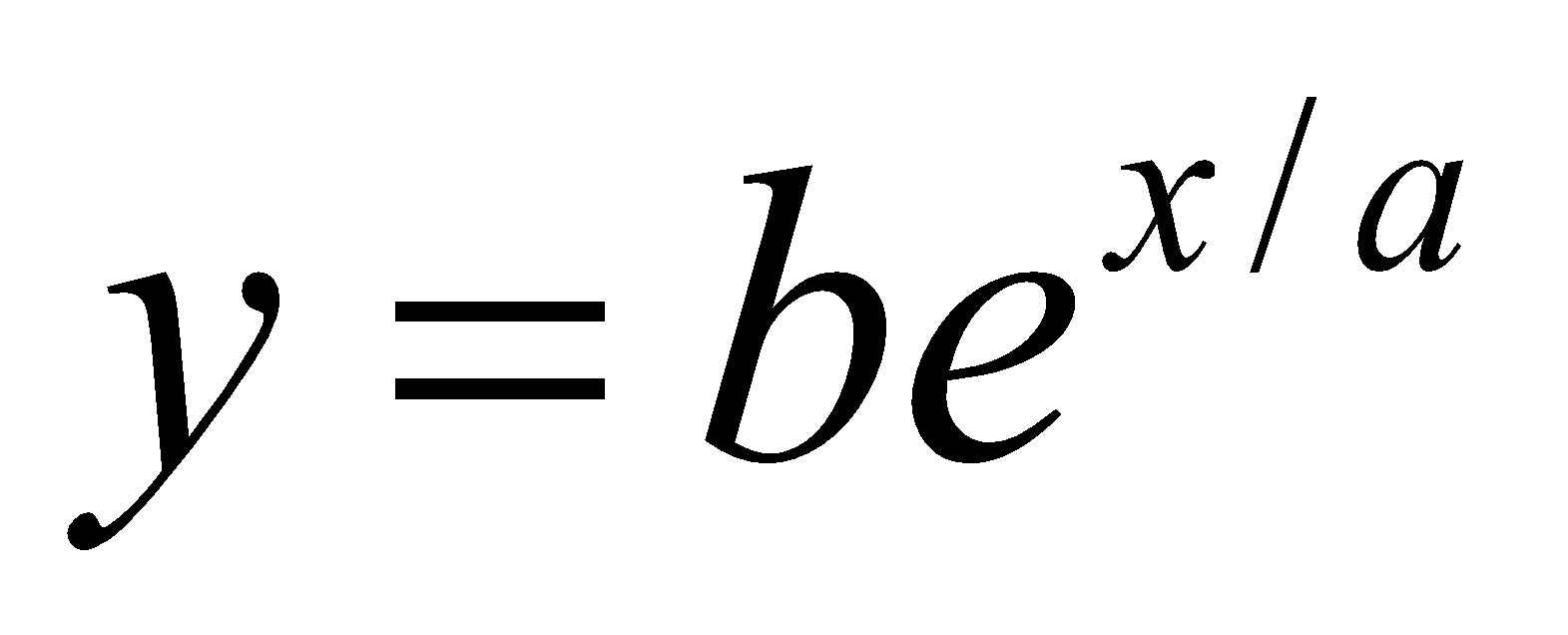 at the point
at the point 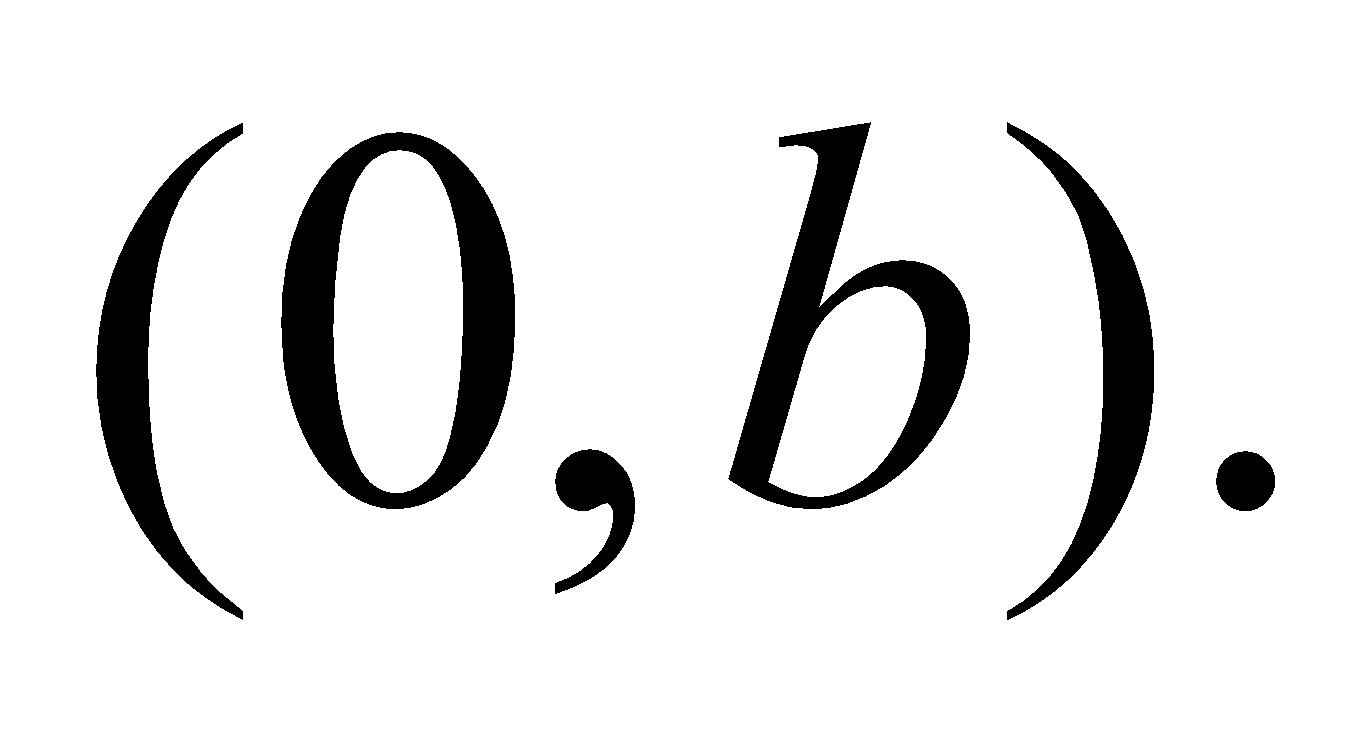 3
3
(d) If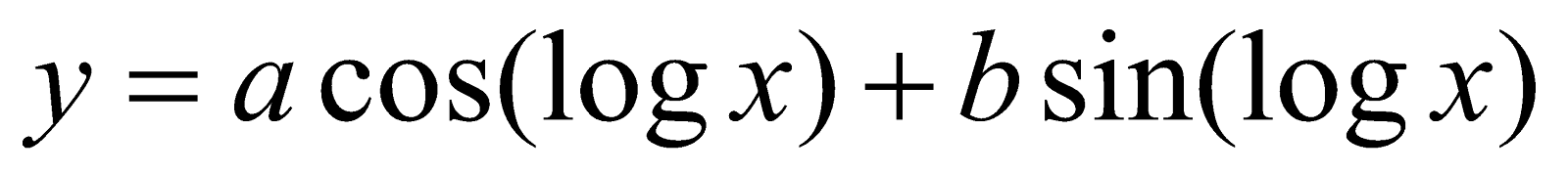 , then show that
, then show that  4
4
Or
Find the radius of curvature at the point  on the cycloid
on the cycloid 
2. (a) Write the statement of Darboux’s theorem. 1
(b) Show that
is continuous at 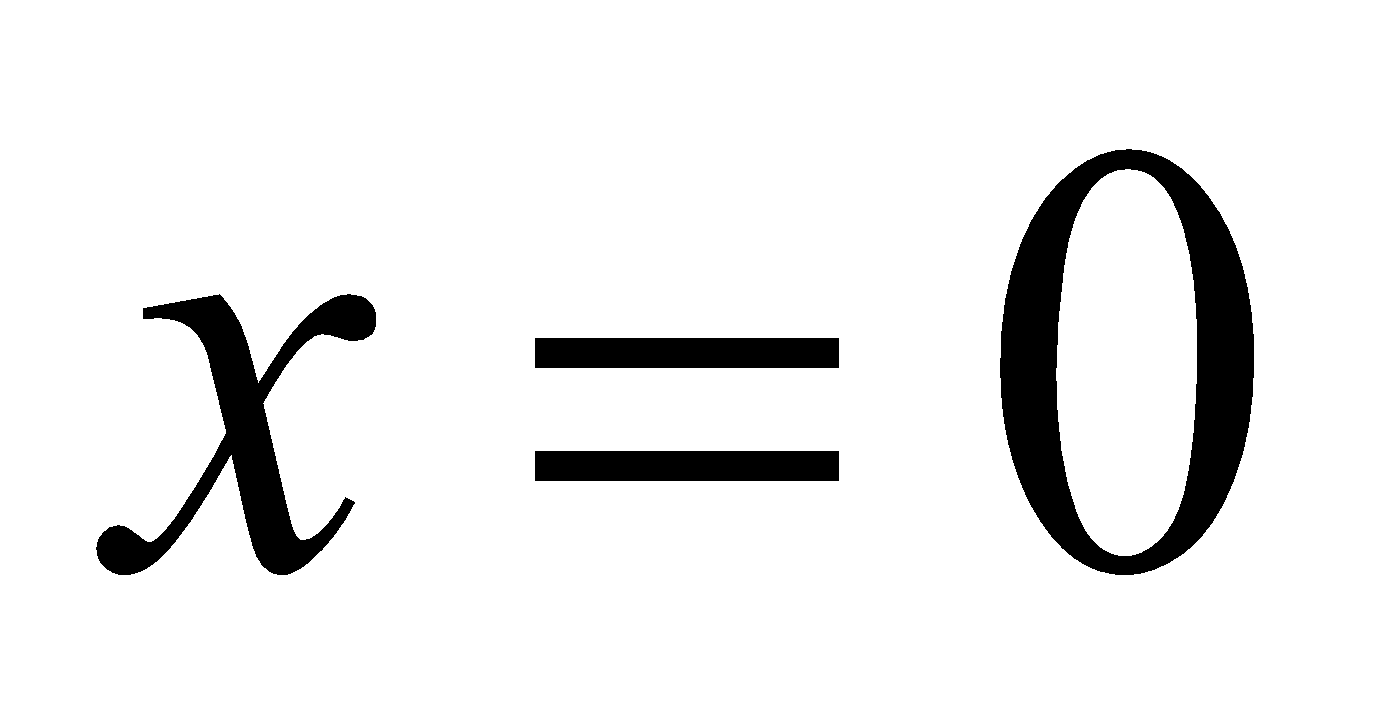 2
2
(c) Show that  4
4
Or
Expand 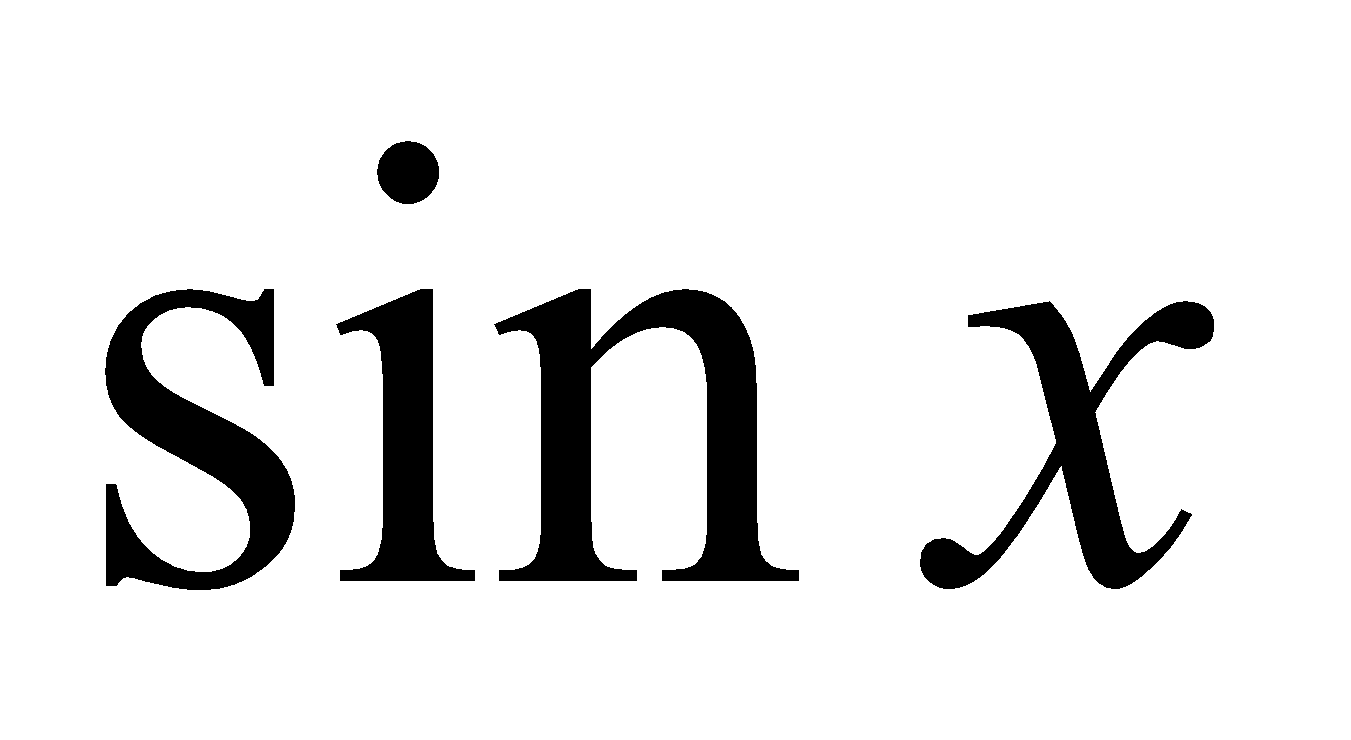 in an infinite series using Maclaurin’s series.
in an infinite series using Maclaurin’s series.
(d) Verify Rolle’s Theorem for  3
3
3. (a) State the Euler’s Theorem on homogeneous function of two variables. 1
(b) If
then show that
Or
If
then show that
4. (a) Write the statement of Schwartz’s theorem. 1
(b) if  and
and 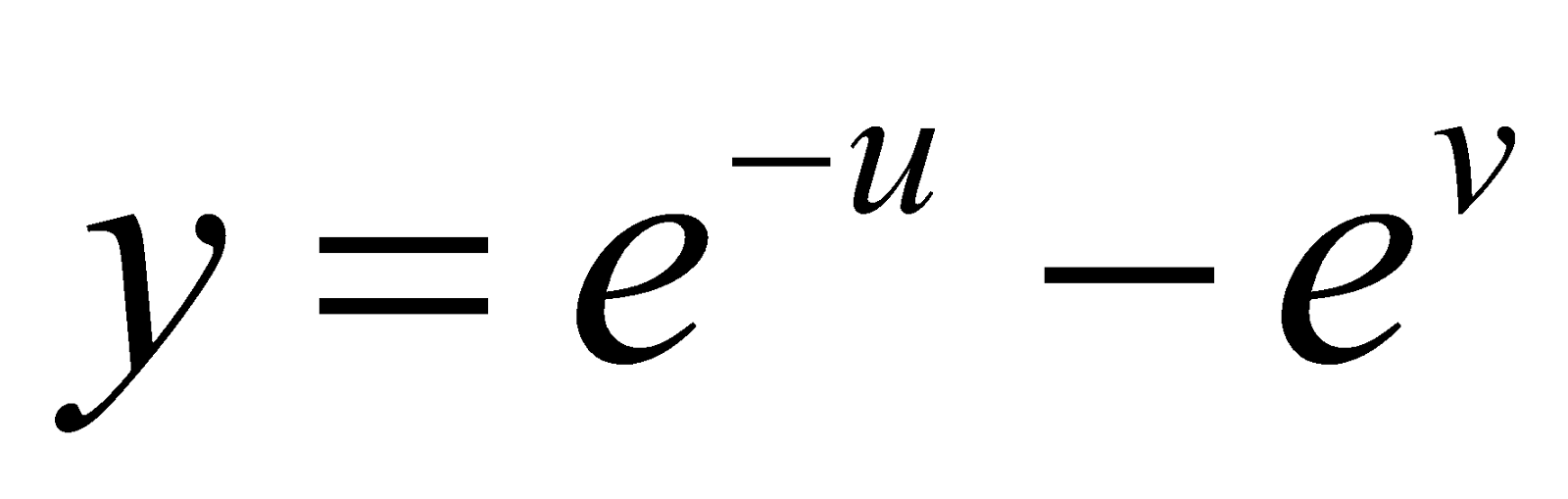 , then show that
, then show that
(c) If z is a function of x and y and , then prove that
, then prove that
Or
Prove that
GROUP – B
(Integral Calculus)
(Marks: 20)
5. (a) Write the value of
(b) Prove that 2
(c) Prove that 3
(d) Show that 4
Or
Using reduction formula, evaluate
6. (a) Write the formula for length of an arc between two points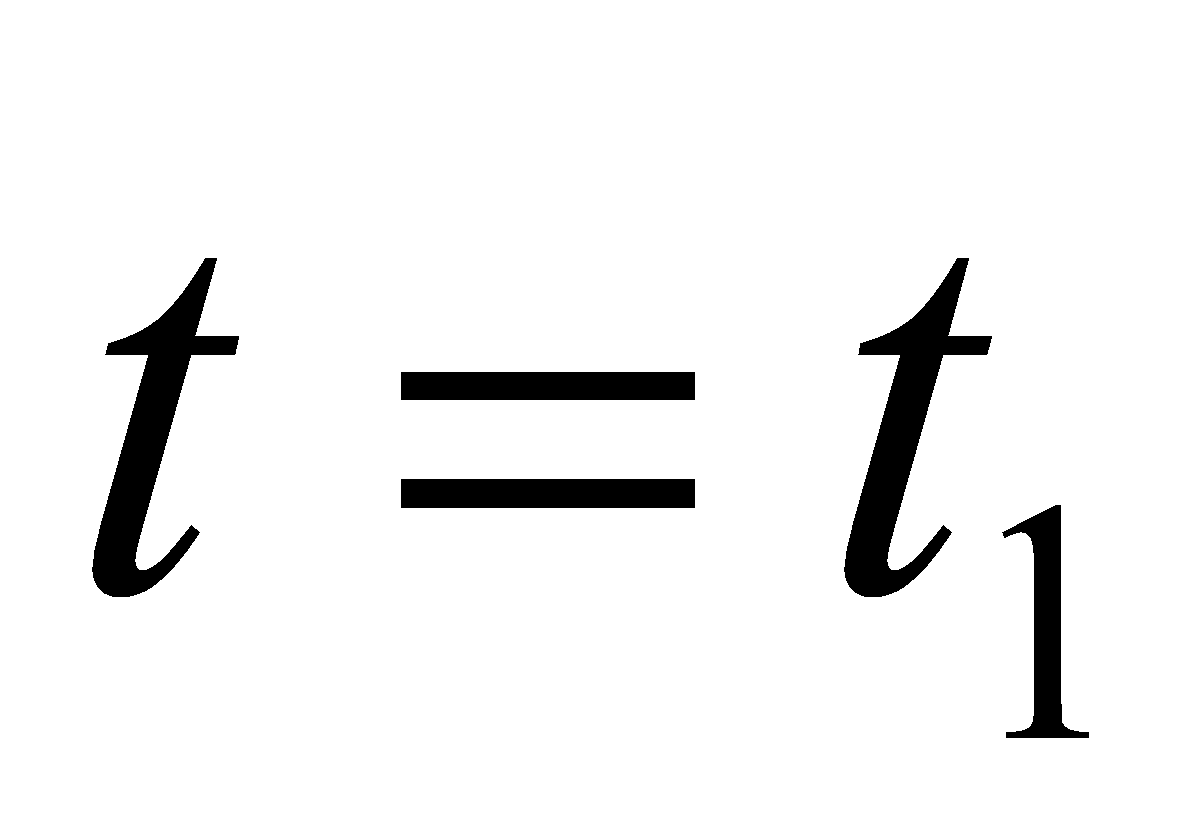 and
and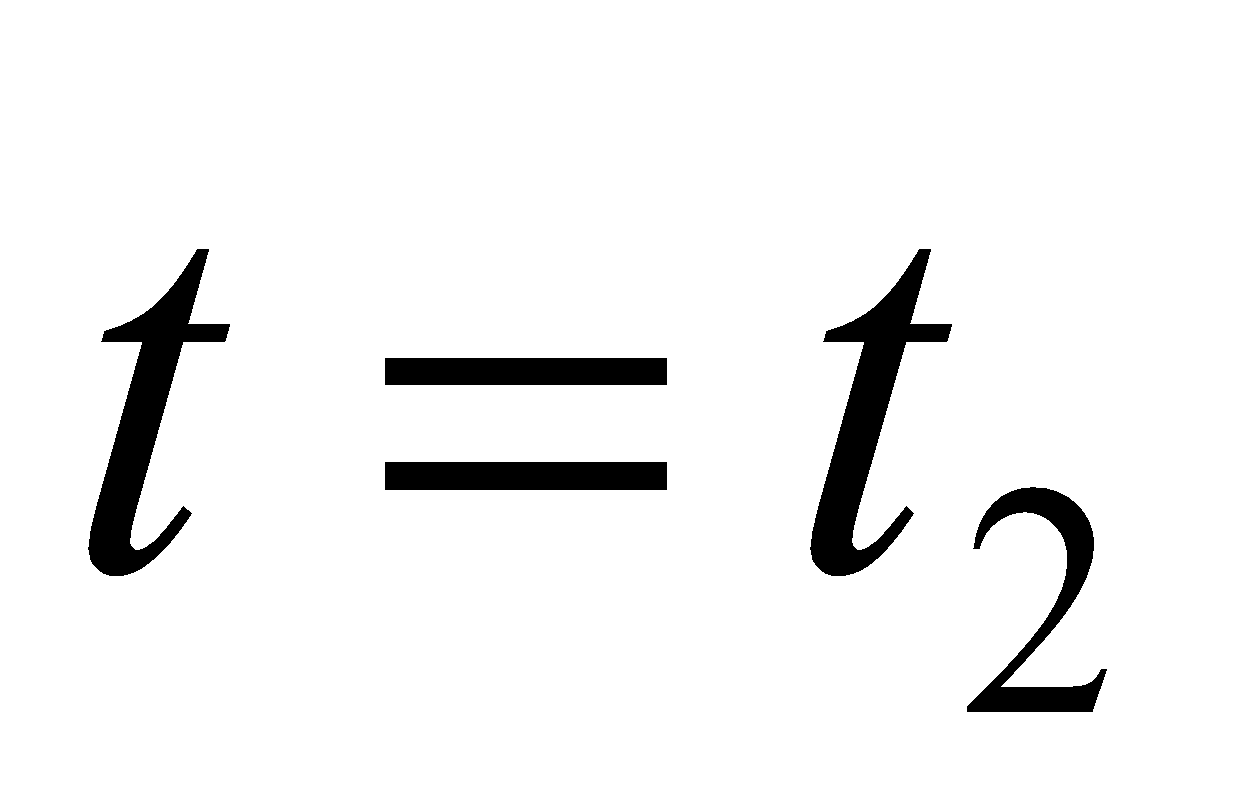 when the curve is given in parametric form. 1
when the curve is given in parametric form. 1
(b) Find the length of the arc of the curve and
and from
from  to
to  4
4
Or
Find the perimeter of the cardioids 
(c) Find the volume and surface area of the solid of revolution formed by rotation of the parabola  about x-axis and bounded by
about x-axis and bounded by 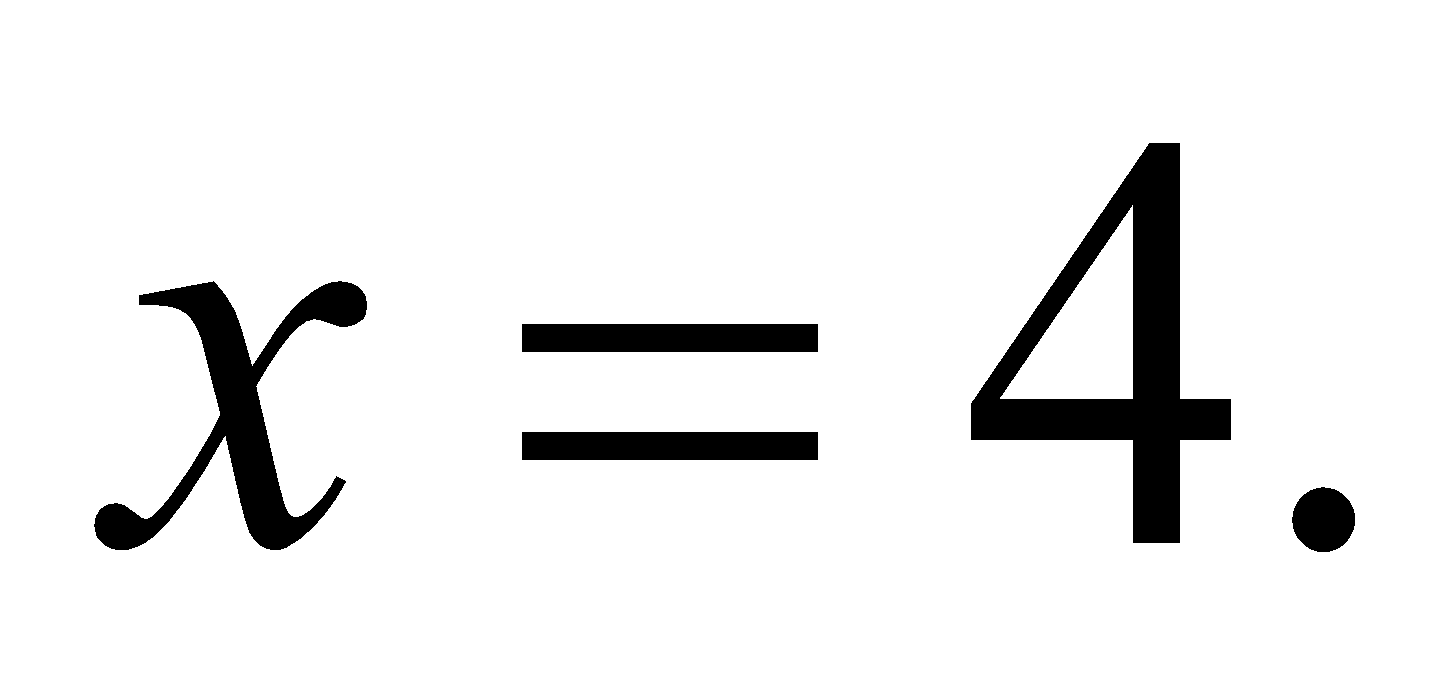 5
5
Or
Find the volume and surface of the solid of revolution of the ellipse
GROUP – C
(Riemann Integral)
(Marks: 25)
7. (a) Every bounded function defined on an interval [a, b] is Riemann integrable. State True or False. 1
(b) Prove that a constant function is always Riemann integrable. 3
(c) State and prove the necessary and sufficient condition for a function to be Riemann integrable. 4
Or
Prove that is a function is monotonic on [a, b], then it is Riemann integrable on [a, b].
8. (a) Define primitive of a function. 1
(b) If  is bounded and integrable in
is bounded and integrable in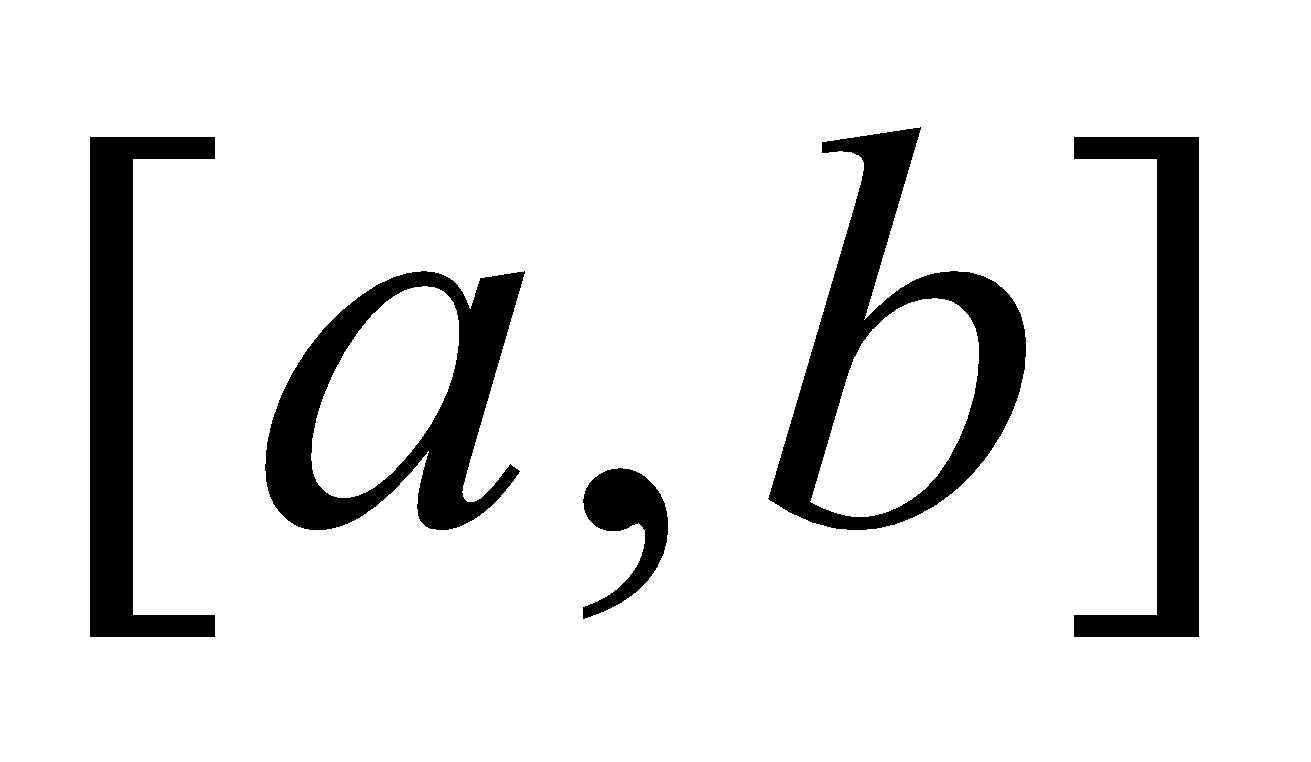 , and
, and 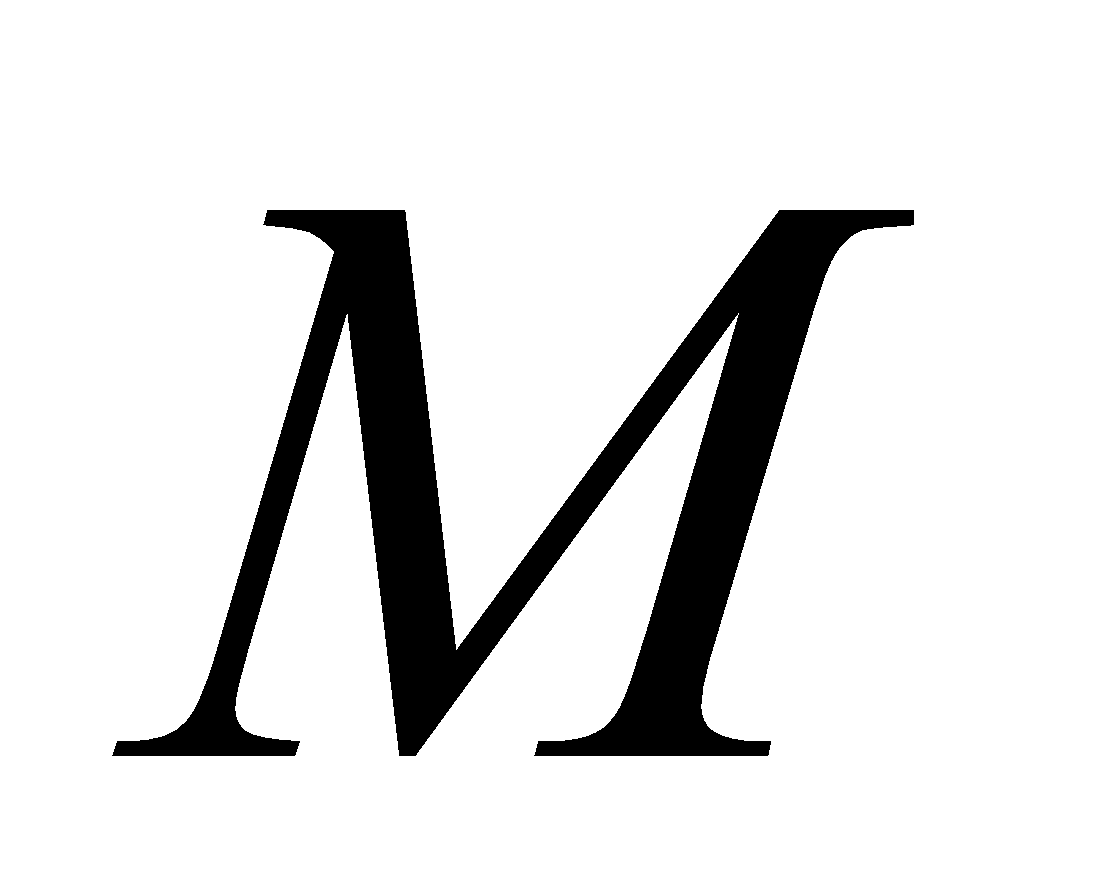 and
and  are the bounds of
are the bounds of  in
in 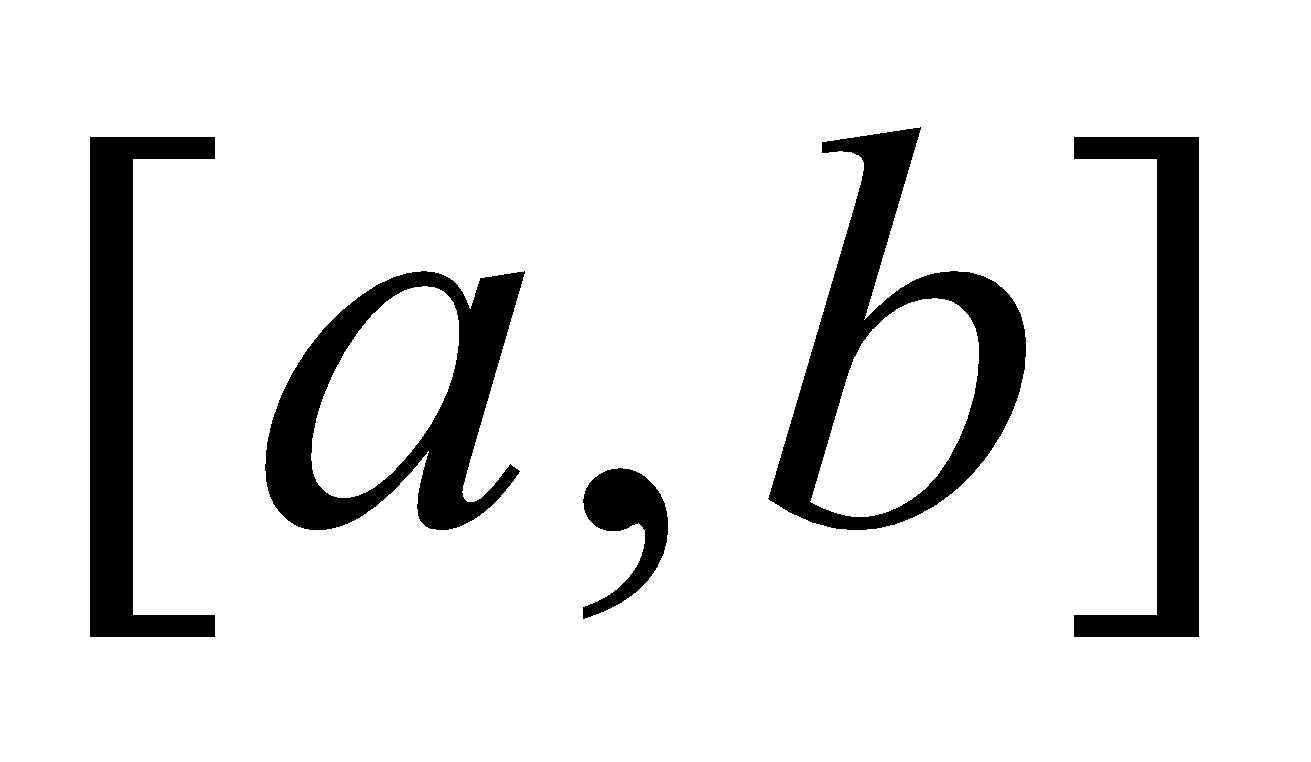 , then prove that
, then prove that
(c) If
Both exist and  keeps the same sign throughout the interval
keeps the same sign throughout the interval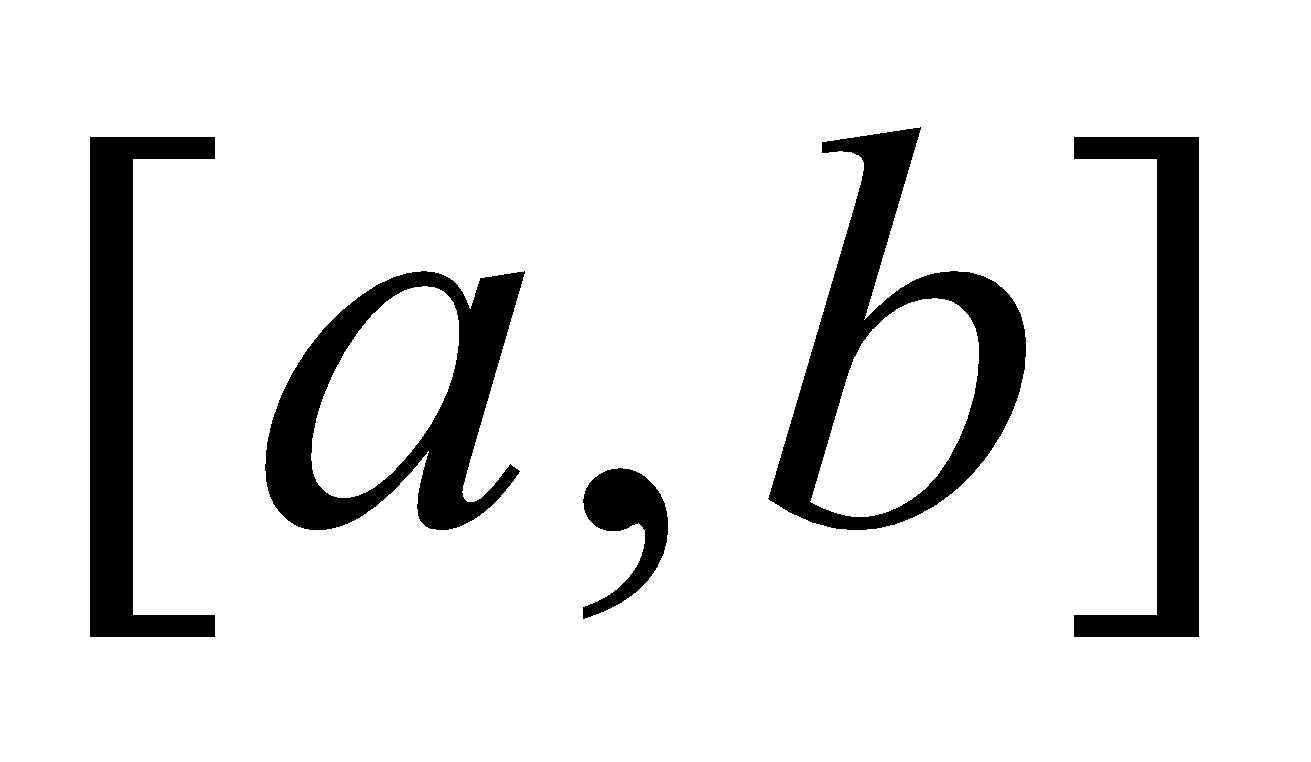 , then prove that there exists a number
, then prove that there exists a number  between the bounds of
between the bounds of  such that
such that
9. (a) Give example of an improper integral of second kind. 1
(b) Test for convergence of 2
(c) Prove that
converges. 3
Also Read: Dibrugarh University Question Papers
10. Answer any one of the following: 4
- Prove that
Hence deduce
- Prove that
***


Post a Comment
Kindly give your valuable feedback to improve this website.