[BA 2nd Sem Question Papers, Dibrugarh University, 2014, Mathematics, Major, Matrices, Ordinary Differential Equations, Numerical Analysis]
2014 (May)
MATHEMATICS (Major)
Course: 201
(Matrices, Ordinary Differential Equations, Numerical Analysis)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
1. (a) State True or False: If
is a non-zero matrix, then rank
. 1
is a non-zero matrix, then rank. 1
(b) Define elementary matrix. Also find the rank of the matrix
considering
. 2
considering. 2
(c) Find the rank of the following matrix reducing it into normal form: 5
Reduce the following matrix
to Echelon form and hence finds its rank:
to Echelon form and hence finds its rank: 
2. (a) Write down the condition under which the system of equations
possesses a unique solution. 1
possesses a unique solution. 1
(b) Show that a characteristic vector of a matrix cannot correspond to more than one characteristic value of. 2
. 2
(c) Show that the only real value of
for which the following equations have non-zero solution is 6: 3
for which the following equations have non-zero solution is 6: 3
(d) Show that the following system of equations is consistent and solve them completely: 2+4=6
State Cayley-Hamilton theorem. Show that the matrix
Satisfies Cayley-Hamilton theorem. 1+5=6
(B) Ordinary Differential Equations
(Marks: 30)
3. (a) Write True or False:
“The singular solution of a differential equation in Clairaut’s from contains only one arbitrary constant.” 1
(b) Find the integrating factor of the differential equation. 2
(c) Solve any one: 3
, where
(d) Use Wronskian to show that the functions
are linearly independent. Determine the differential equation with these as independent solutions. 4
are linearly independent. Determine the differential equation with these as independent solutions. 4
Or
Show that the Wronskian of the functionsand 
is non-zero. Can these functions be independent solutions of an ordinary differential equation? If so, determine this differential equation.
and is non-zero. Can these functions be independent solutions of an ordinary differential equation? If so, determine this differential equation.
4. (a) What is the auxiliary equation of the differential equation. 1
Where
and
are constant?
and are constant?
(b) Define linear homogeneous equation. 1
(c) Solve any two: 4x2=8
(d) Solve any two: 5x2=10
(By removing 1st order derivative)
(By changing the independent variable)
(By the method of variation of parameters)
(C) Numerical Analysis
(Marks: 30)
5. (a) State True or False: The bisection method always converges. 1
(b) Write the basic difference between the bisection method and method of false position. 1
(c) Explain the geometrical interpretation of the Newton-Raphson method for solving an algebraic equation. 3
(d) Answer any two: 5x2=10
- Describe the regula-falsi method for obtaining a real root of an algebraic equation.
- By using Newton-Raphson method, find the root of
, which is nearer to
, correct to three decimal places by performing at least 3 iterative.
- Solve the following equations by Gauss elimination method:
Also Read: Dibrugarh University Question Papers
6. (a) State True or False: Simpson’s one-third rule is better than the trapezoidal rule. 1
(b) Evaluate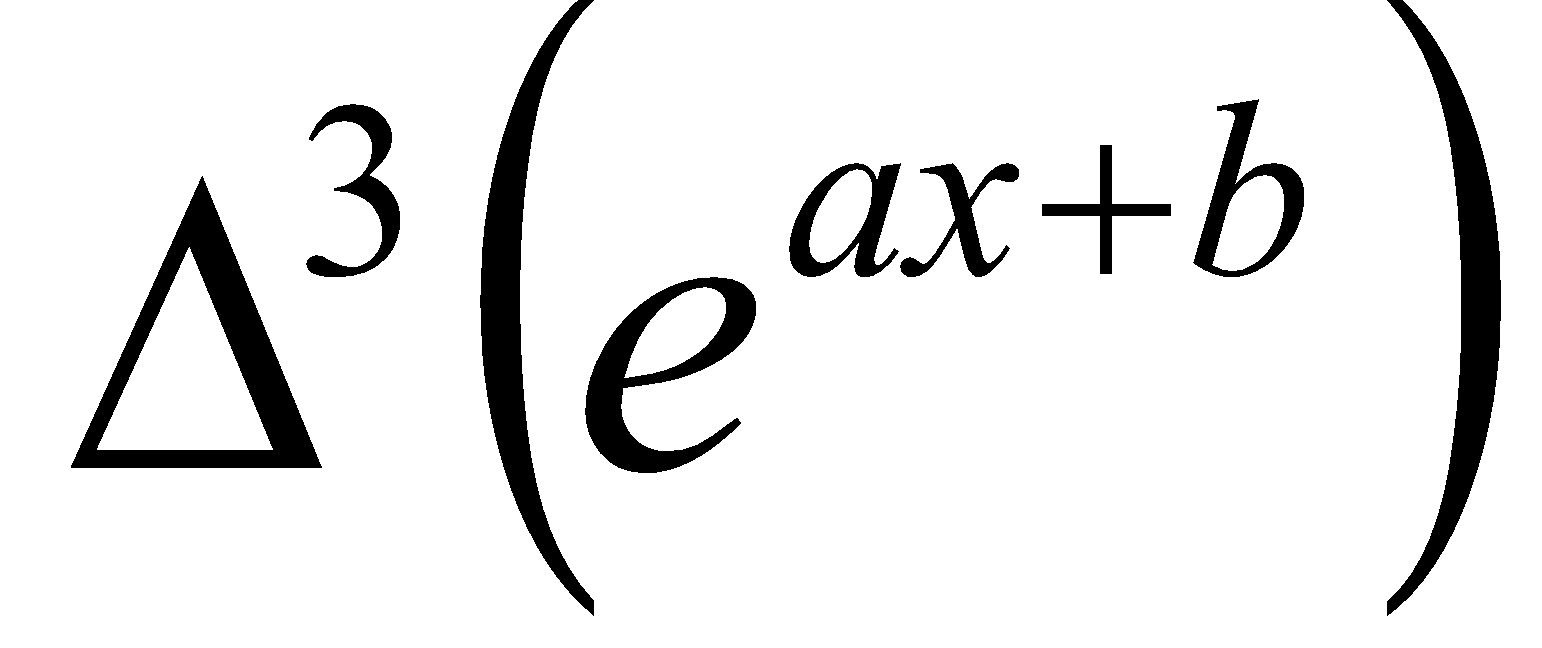 
the interval of differencing being
. 2
the interval of differencing being. 2
(c) Show that
, where the symbols have their usual meanings. 2
, where the symbols have their usual meanings. 2
(d) Answer any two of the following: 5x2=10
- Deduce Lagrange interpolation formula.
- Estimate the missing term in the following table:
 : |
0
|
1
|
2
|
3
|
4
|
 : |
1
|
3
|
9
|
?
|
81
|
- Show that
by dividing the range into 10 equal parts.
***
Post a Comment
Kindly give your valuable feedback to improve this website.