[BA 3rd Sem Question Papers, Dibrugarh University, 2015, Mathematics, General, Group - A: Coordinate Geometry and Group - B: Analysis - I (Real Analysis)]
GROUP – A
(Coordinate Geometry)
SECTION – I
(2 –Dimension)
1. (a) Write the condition under which the conic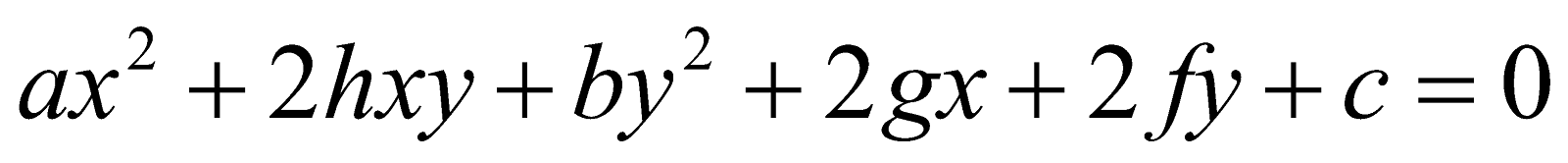 
is non-singular. 1
is non-singular. 1
(b) Find the new coordinates of the point
, if the frame of reference is rotated through an angle
, without changing the origin. 2
, if the frame of reference is rotated through an angle, without changing the origin. 2
(c) Find the angle through which it is to be rotated to remove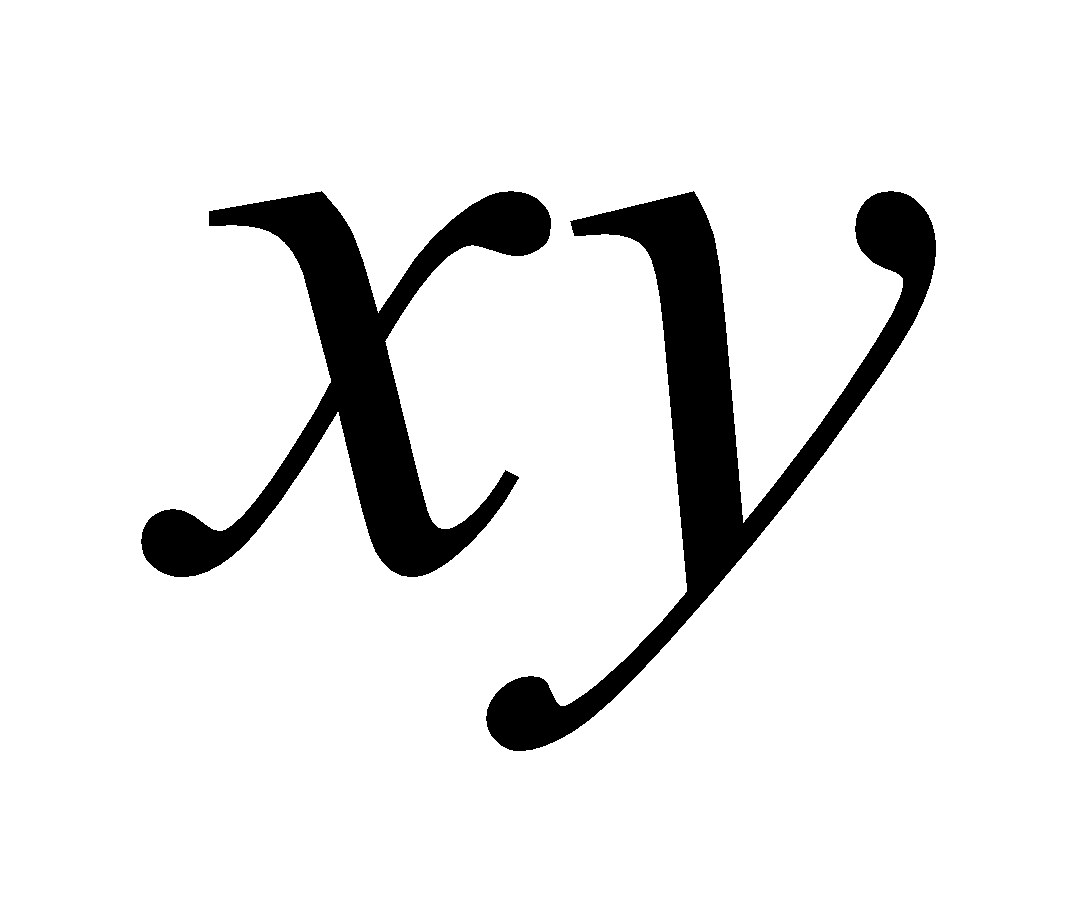 
term from
. 2
term from. 2
2. (a) 
represents a pair of straight lines. Determine whether they are parallel or perpendicular to each other. 1
represents a pair of straight lines. Determine whether they are parallel or perpendicular to each other. 1
(b) Find the angle between the pair of lines
. 2
. 2
(c) Find the pair of lines represented by
. 3
. 3
(d) Show that the lines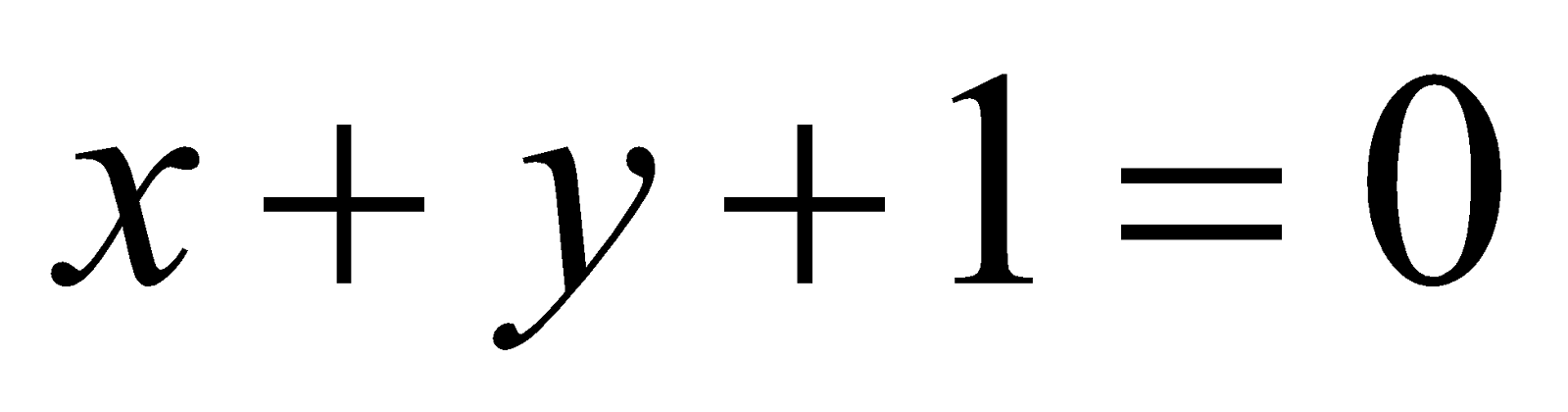 
and
form an equilateral triangle. 6
andform an equilateral triangle. 6
Or
Discuss the nature of the conic represented by the equation
and reduce it to canonical form.
3. (a) Find the equation of tangent at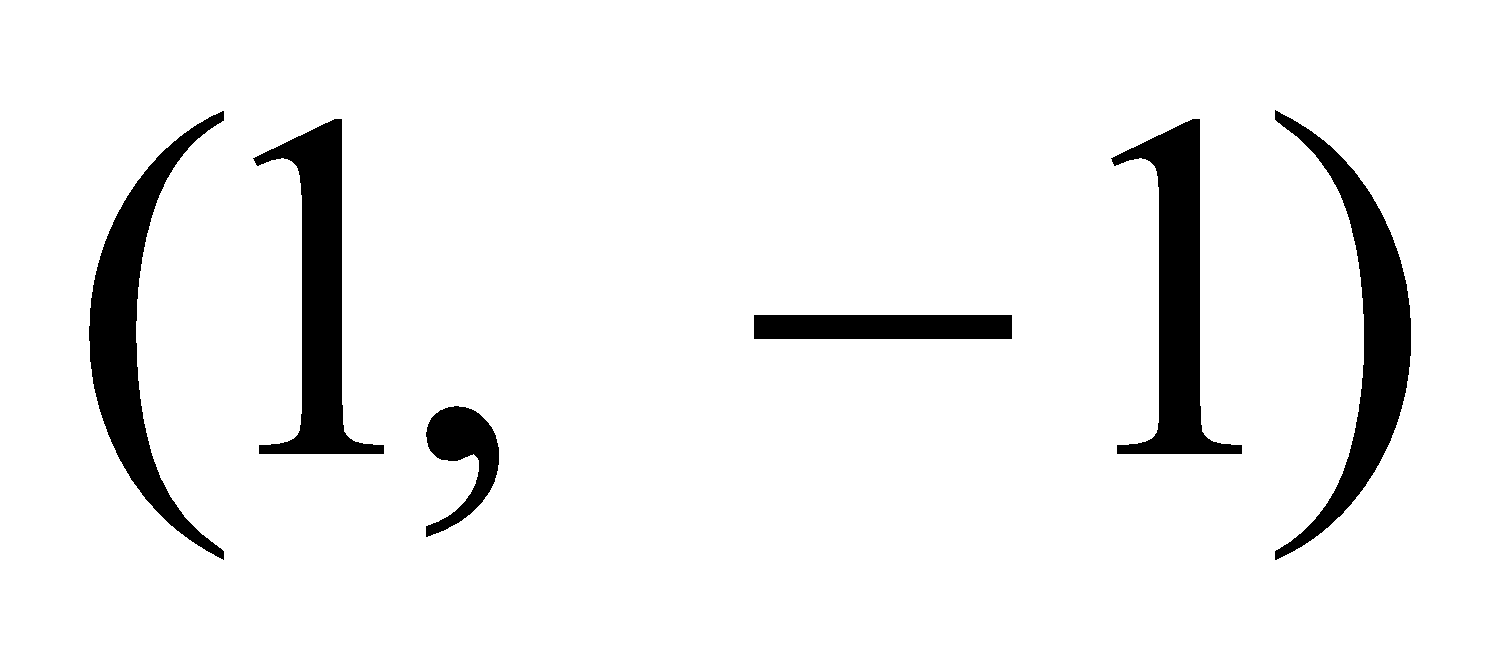 
to the conic 
. 2
to the conic . 2
(b) Find the centre of the conic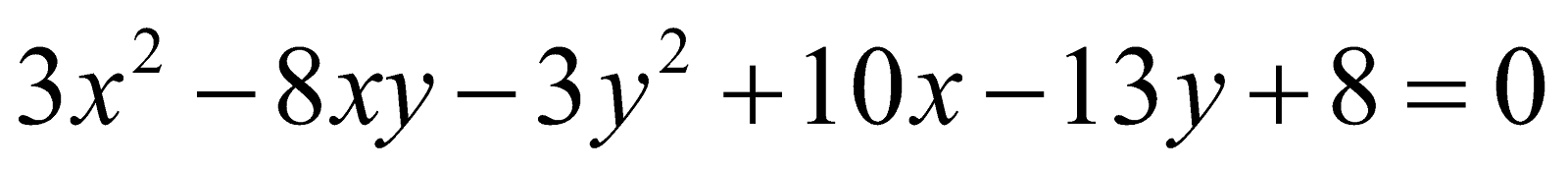
. 3
. 3
(c) Find the pole of a given line with respect to a conic. 5
Or
Determine whether the conic represented by
has a single centre, infinitely many centres or no centre.
SECTION – II
(3-Dimension)
4. (a) Plane is described by an equation. Write the degree of the equation. 1
(b) The plane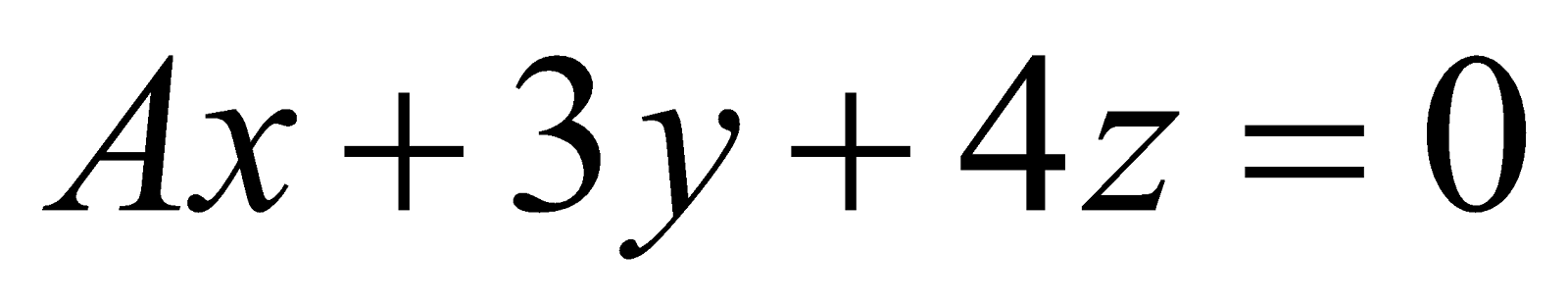 
passes through a particular point. Write the coordinates of that point. 1
passes through a particular point. Write the coordinates of that point. 1
(c) Find the intercepts on the axes made by the plane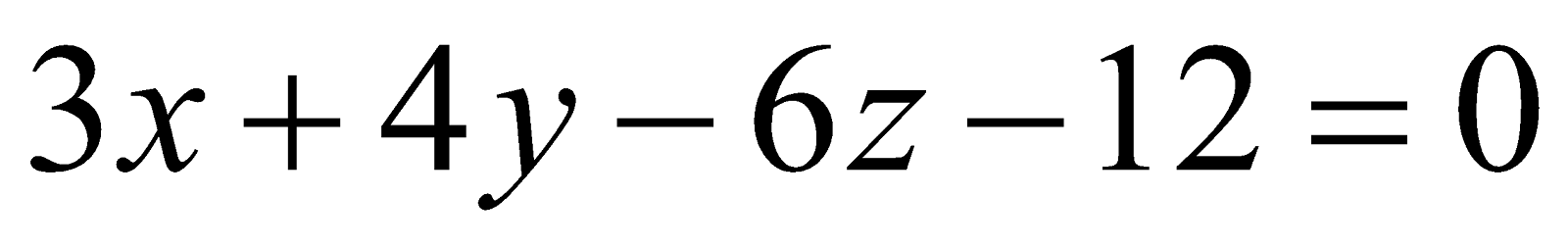
. 2
. 2
(d) Find the equation of the plane passing through the points (3, 1, 1) and (1, -2, 3), and parallel to x-axis. 3
Or
Find the angle between the planes 
and
.
and.
(e) Find the equation of the line in symmetric form passing through (2, 0, 4) and (1, -2, 3). 3
5. (a) Find the length of the shortest distance between the following lines: 4
(b) Find the equation of the perpendicular line to the lines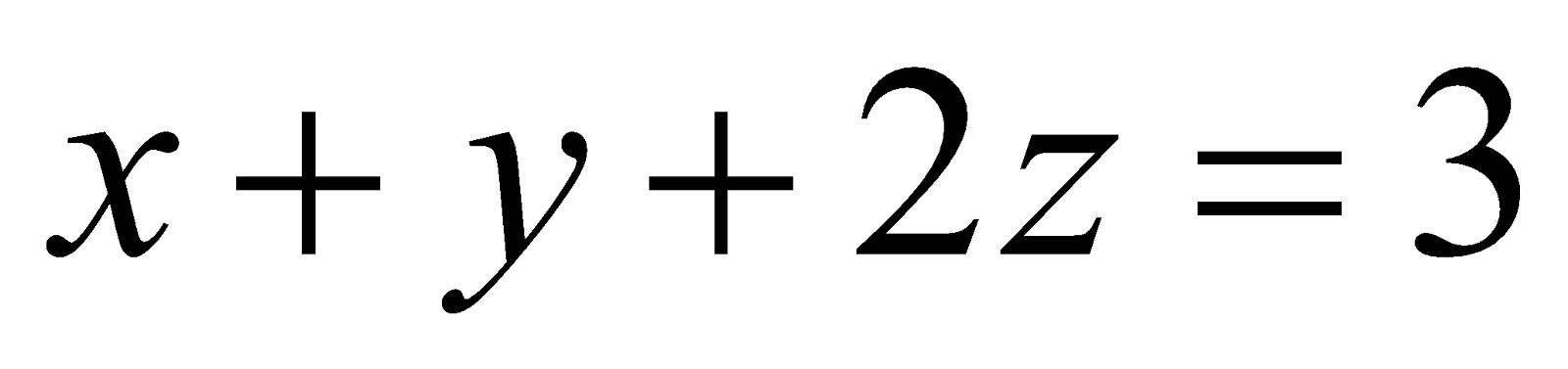
;
and z-axis. 4
;and z-axis. 4
GROUP – B
(Analysis – I)
6. (a) If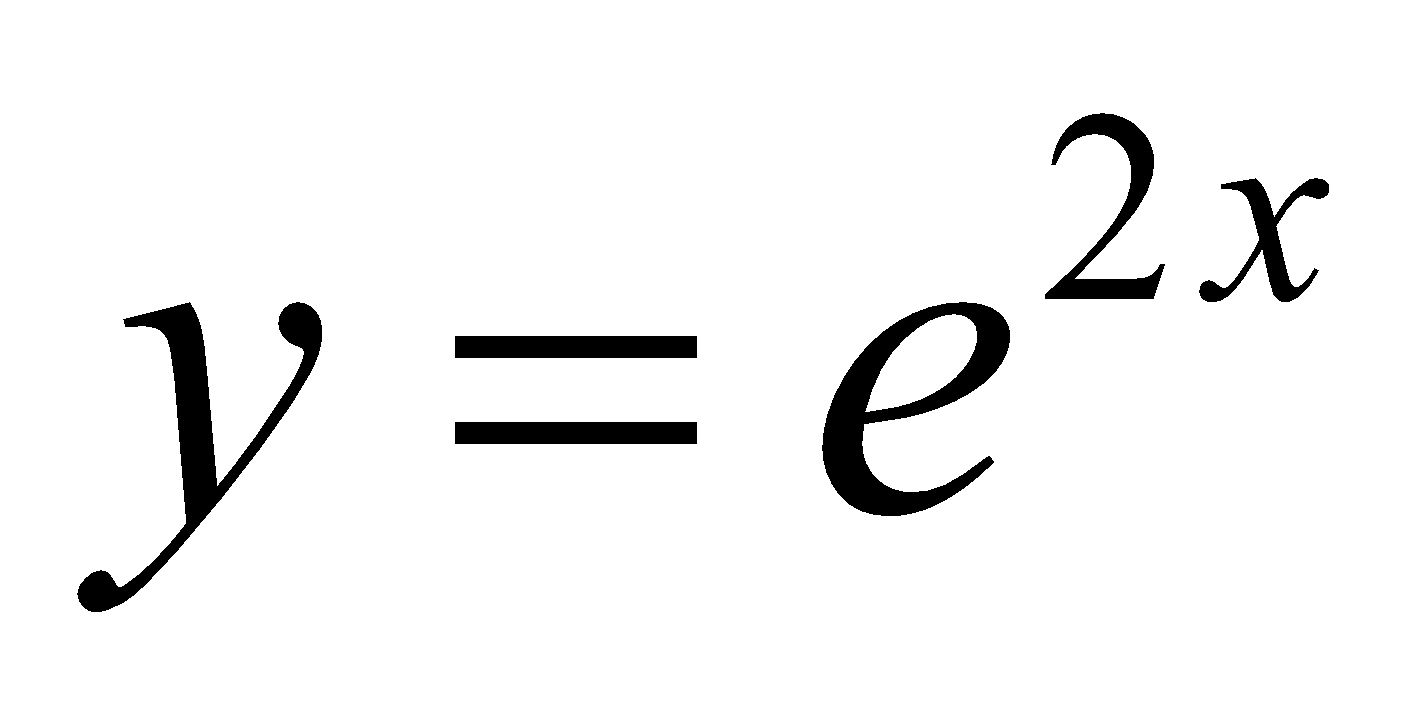 
, then find the value of
. 1
, then find the value of. 1
(b) If
, then find the value of. 2
, then find the value of. 2
(c) Find the length of subtangent to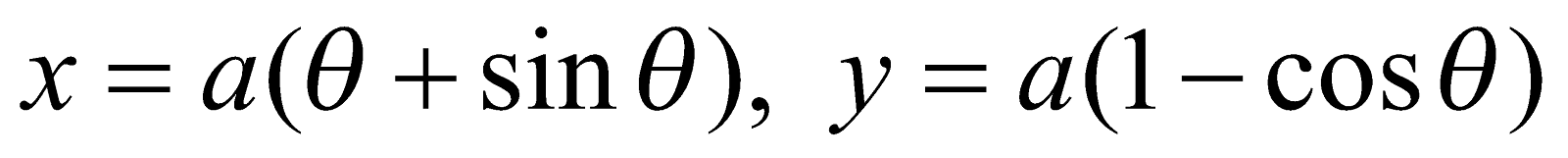 
at
. 3
at. 3
Or
Find the radius of curvature of 
at any point
.
at any point.
(d) Evaluate any one of the following: 4
7. (a) Write Maclaurin’s theorem with Lagrange’s form of remainder. 1
(b) Write the geometrical meaning of Lagrange’s mean value theorem. 2
(c) Show that a function, which is derivable at a point, is continous at that point. 2
(d) State and prove Rolle’s Theorem. 5
Or
If a function 
is derivable on a closed interval 
and
, 
are of opposite signs, then there exists at least one point 
between 
and 
such that
.
is derivable on a closed interval and, are of opposite signs, then there exists at least one point between and such that.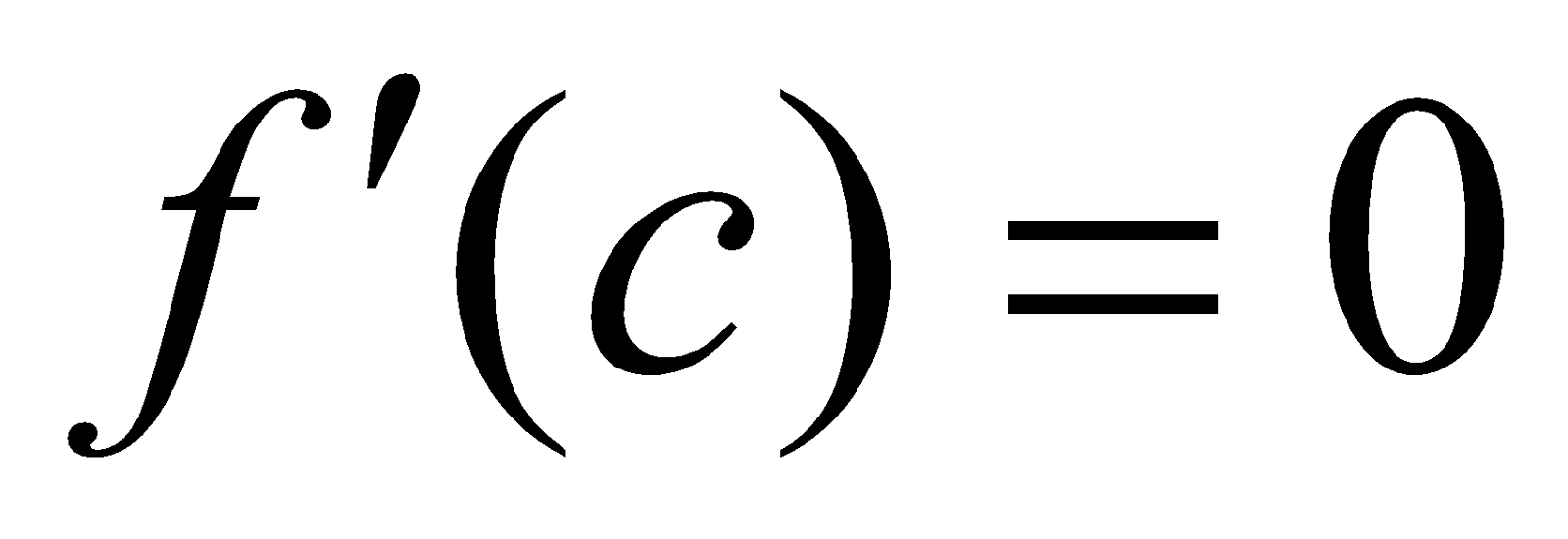
8. (a) If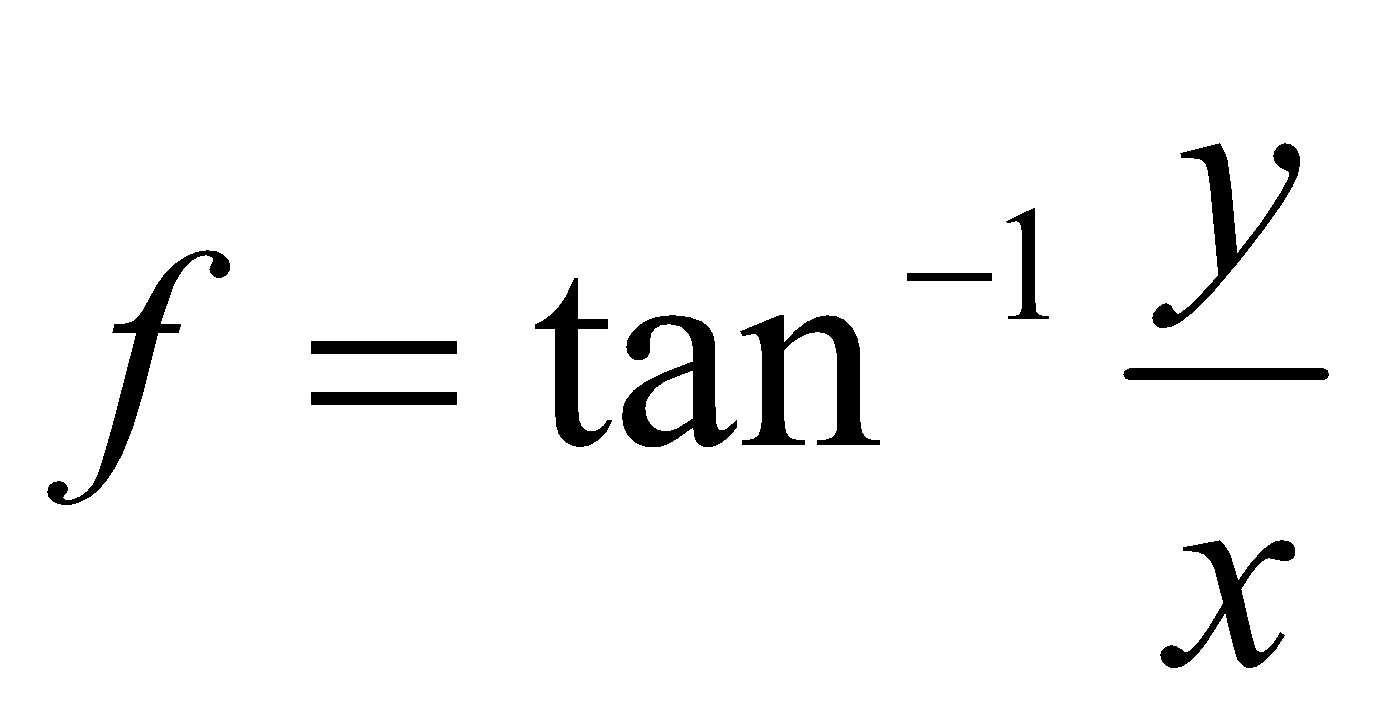 
, then find 
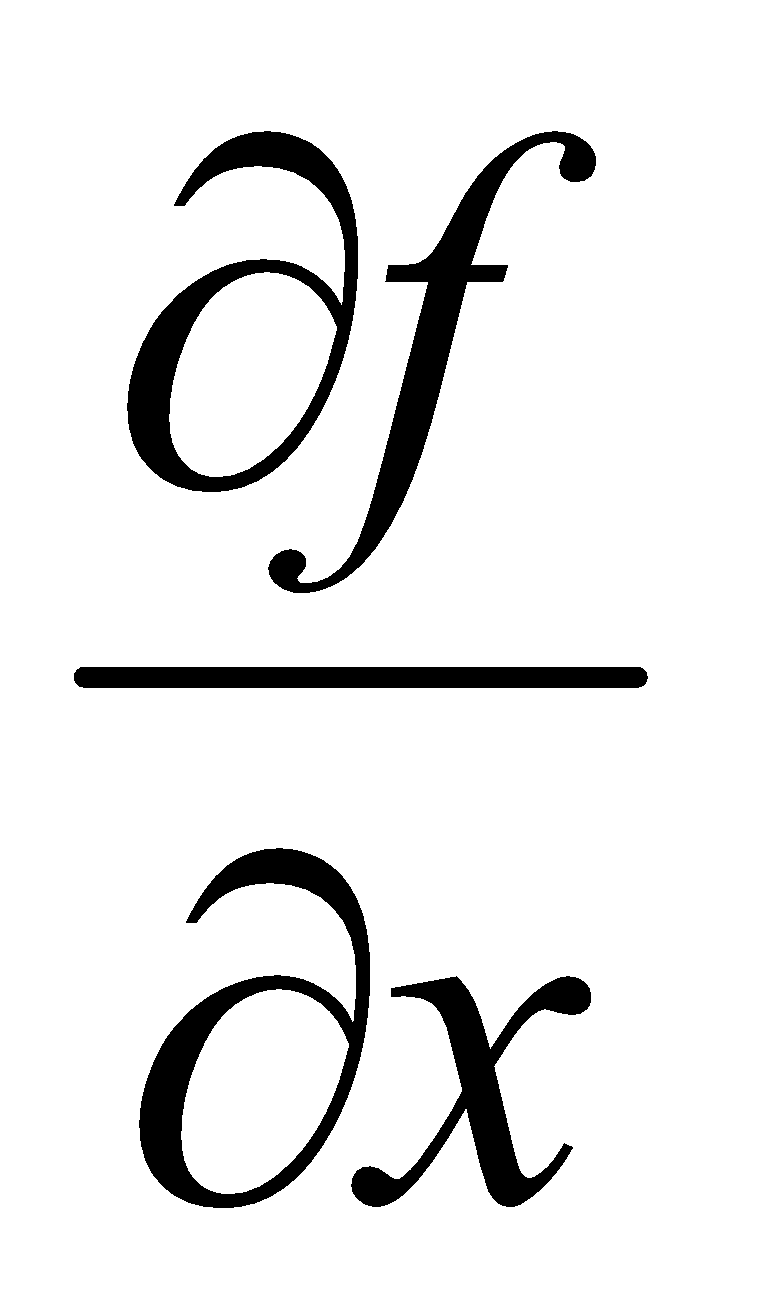. 1
, then find . 1
(b) Verify Euler’s theorem for
. 4
. 4
Or
If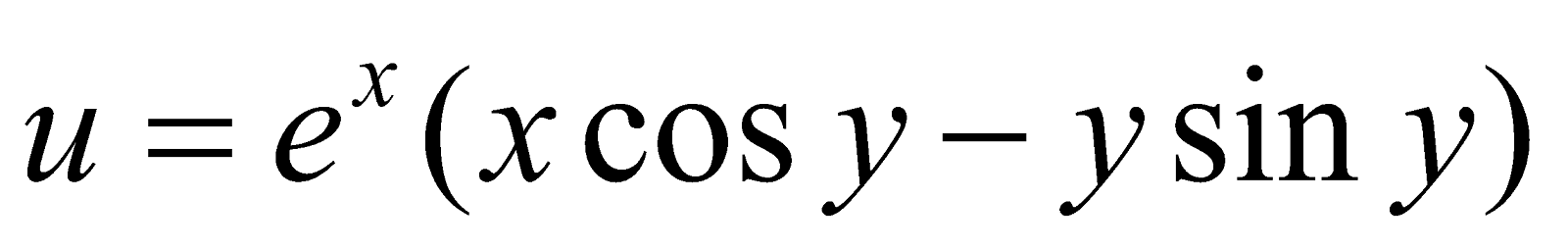 
, then show that 
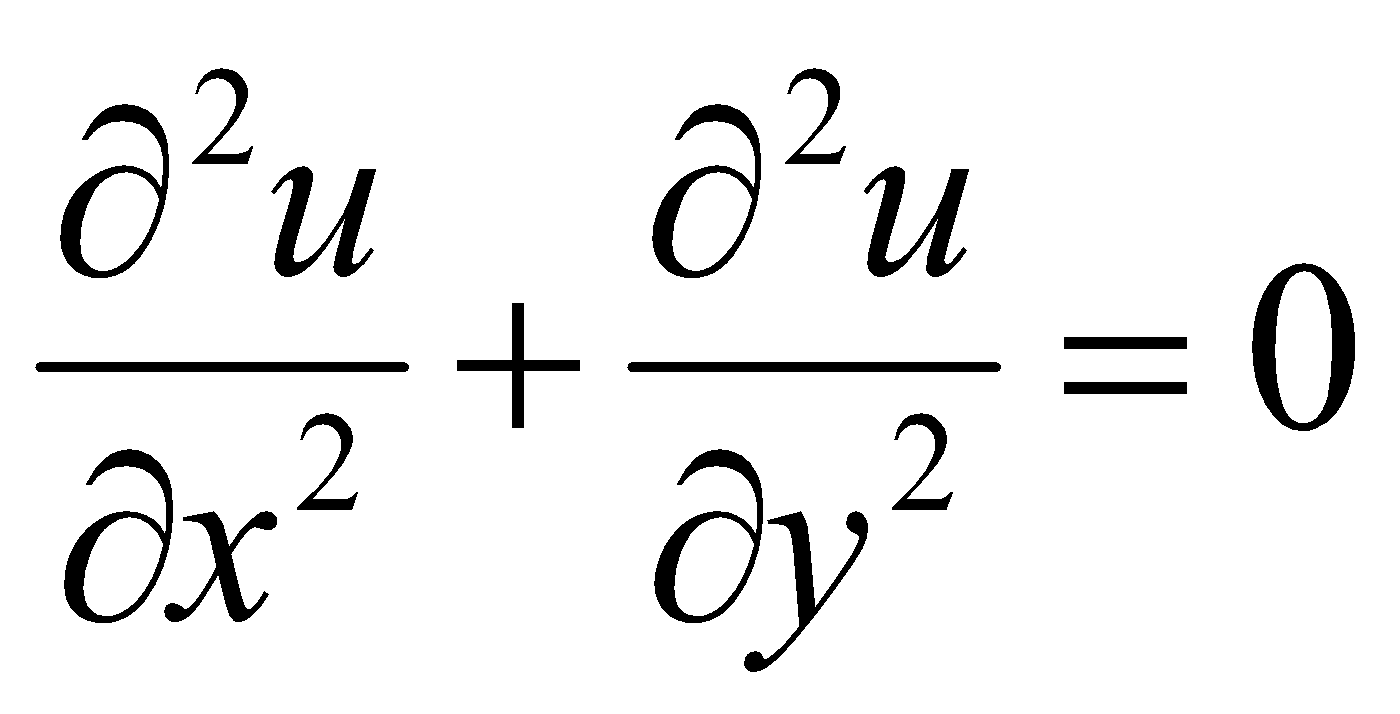. 1
, then show that . 1Also Read: Dibrugarh University Question Papers
9. (a) Write the condition when 
.
.
(b) Evaluate any one of the following: 4
(c) Obtain the reduction formula for
. 5
. 5
Or
Find the perimeter of the asteroid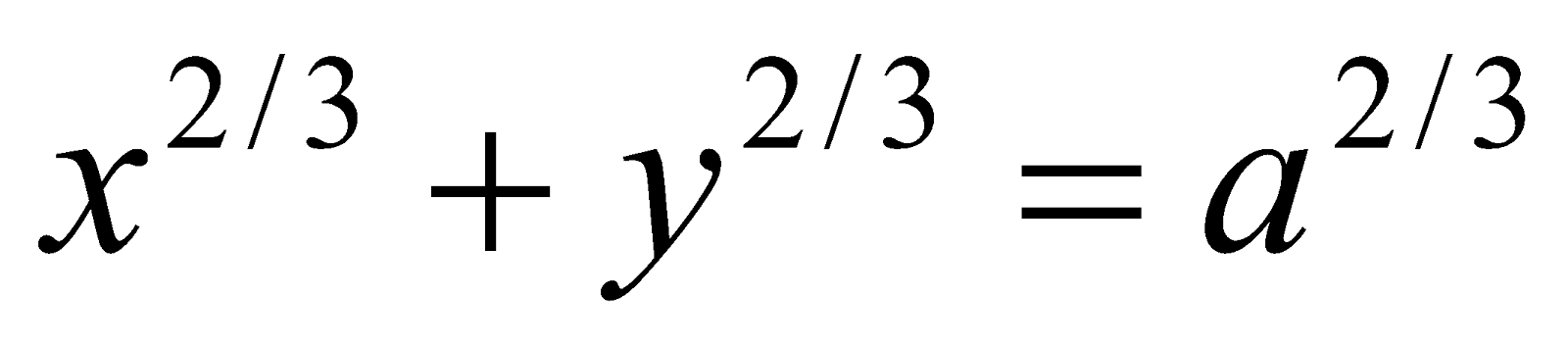
.
.
***
Post a Comment
Kindly give your valuable feedback to improve this website.