[BA 3rd Sem Question Papers, Dibrugarh University, 2014, Mathematics, General, Group - A: Coordinate Geometry and Group - B: Analysis - I (Real Analysis)]
GROUP – A
(Coordinate Geometry)
SECTION – I
(2-Dimension)
1. (a) Write what should be done to remove 
term from the equation 
. 1
term from the equation . 1
(b) Write the transformed equation of the straight line 
when the origin is transformed to the point
.
when the origin is transformed to the point.
(c) Find the angle through which the axes must be turned to remove the term from the equation
.
term from the equation.
2. (a) Straight lines represented by 
pass through the origin. State true or false.
pass through the origin. State true or false.
(b) Show that straight lines represented by 
are parallel.
are parallel.
(c) Show that the equation 4
represents a pair of straight lines.
(d) Show that the area of the triangle formed by the lines 
and 
is 5
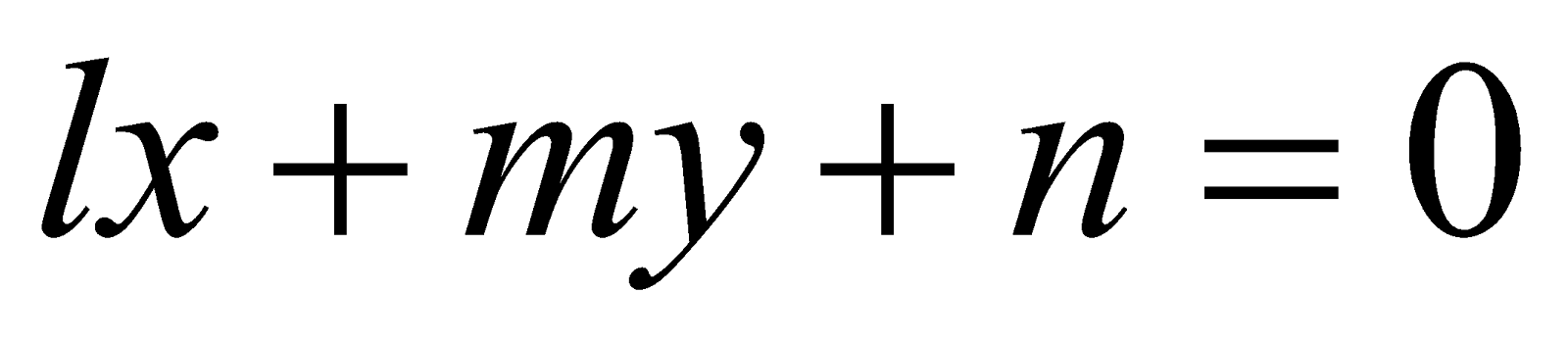and is 5
Or
Show that the lines 
and 
form an equilateral triangle.
and form an equilateral triangle.
3. (a) Let 
and 
for the conic 
. Write the name of the conic. 1
and for the conic . Write the name of the conic. 1
(b) Find the equation of the tangent at 
to the conic
. 2
to the conic. 2
(c) Write the definition of a diameter of a conic. 1
(d) Show that the equation 3
represents a hyperbola.
(e) Show that the sum of the squares of two conjugate semi-diameters of a conic is constant. 3
Or
Determine the nature of the conic
. Also find the centre of the conic.
. Also find the centre of the conic.
SECTION – II
(3-Dimension)
4. (a) Find the intercepts made by the plane 
on the axes. 1
on the axes. 1
(b) Express the equation of the plane 
in normal form. 2
in normal form. 2
(c) Find the equation to the plane through the point 
and normal to the straight line joining the points 
and
. 3
and normal to the straight line joining the points and. 3
Or
Find the coordinates of the point, where the line 
meets the plane
.
meets the plane.
(d) Find the distance of the point of intersection of the line 
and the plane 
from the point
.
and the plane from the point.
5. (a) Define skew lines. 1
(b) Find the shortest distance between the planes 
and
. 2
and. 2
(c) Find the shortest distance between the lines 
and
. 5
and. 5
GROUP – B
(Analysis – I)
6. (a) If 
, then write the value of
1
, then write the value of 1
(b) If 
then find the length of sub tangent of the curve. 1
then find the length of sub tangent of the curve. 1
(c) Find the radius of curvature at any point 
on the curve 
2
on the curve 2
(d) If 
then find the value of 
3
then find the value of 3
(e) Evaluate: 3
Or
If 
then find the value of
then find the value of
7. (a) Write when a function is derivable in a closed interval 
. 1
. 1
(b) Write the geometrical interpretation of Lagrange mean value theorem. 2
(c) Prove that if a function 
is continuous on 
and
, then it assumes every value between 
and
. 4
is continuous on 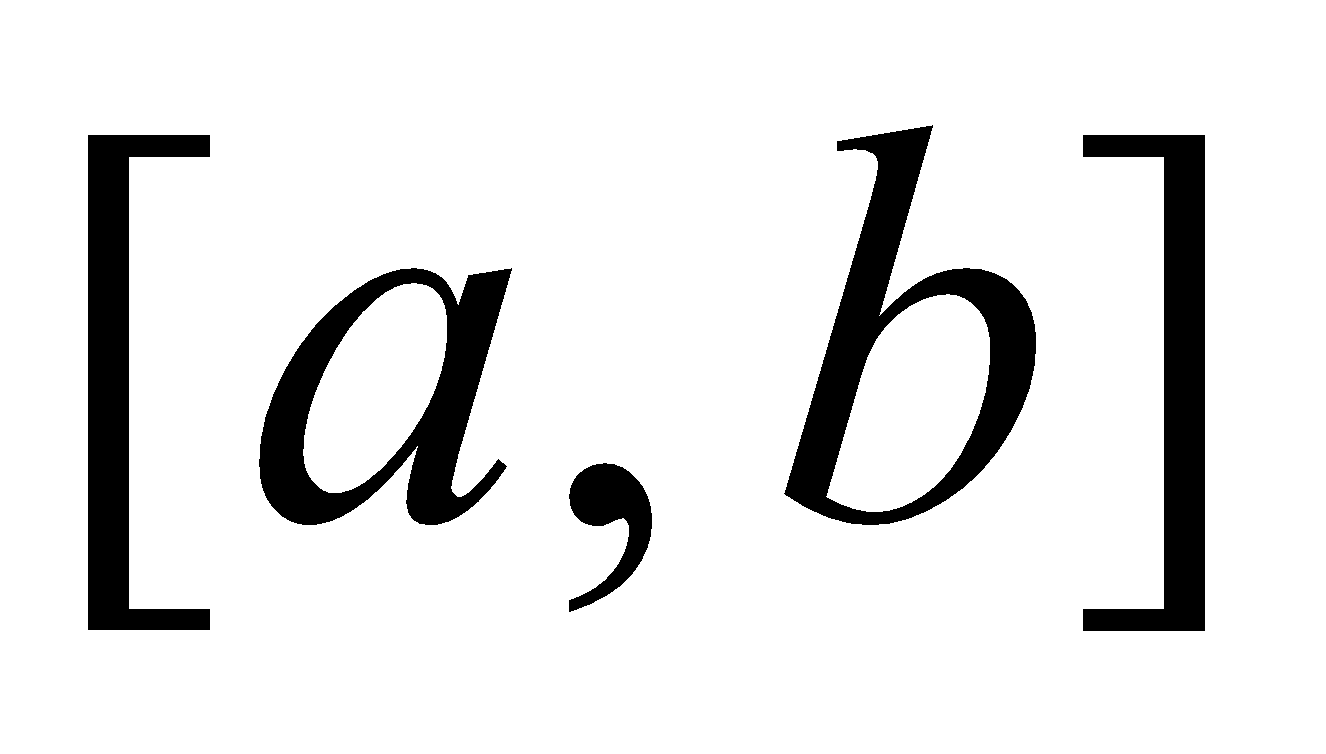and, then it assumes every value between and. 4
(d) Discuss the applicability of Rolle’s Theorem to 
in
. 3
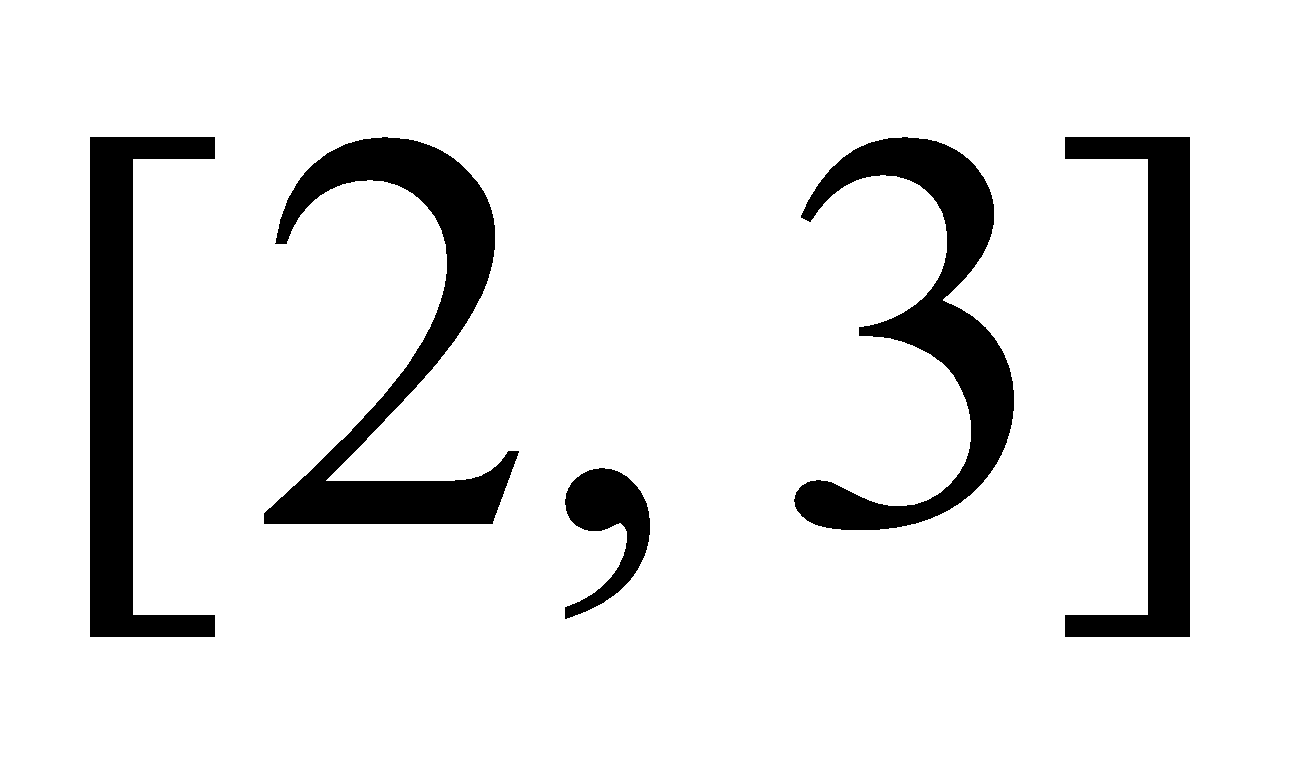in. 3
Or
Expand
by Maclaurin’s theorem with Lagrange form of remainder.
by Maclaurin’s theorem with Lagrange form of remainder.
8. (a) If 
, then find 
2
, then find 2
(b) If
, then show that 
3
, then show that 3
Or
If 
then show that 
then show that 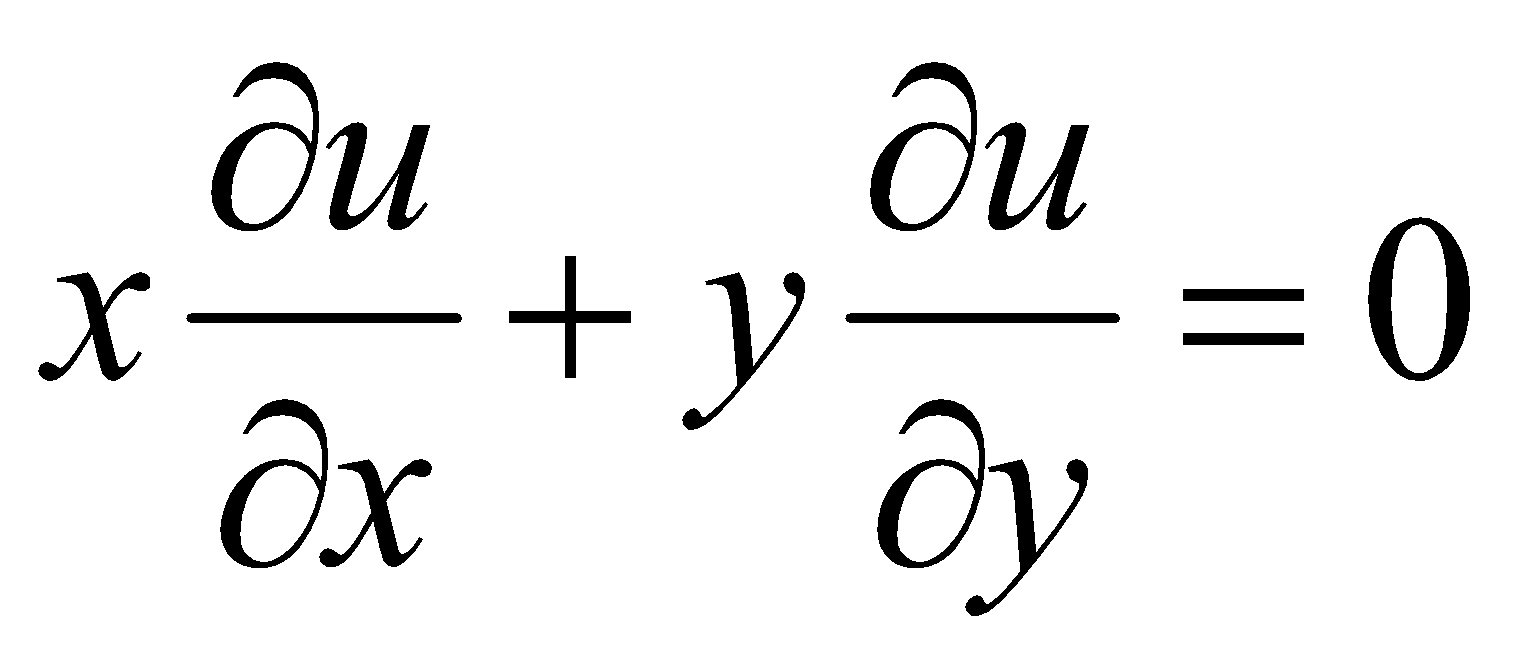Also Read: Dibrugarh University Question Papers
9. (a) Write the condition when 
1
1
(b) Evaluate: 
5
5
(c) Evaluate: 
4
4
Or
Find the length of the curve 
from 1 to 2.
from 1 to 2.
***
Post a Comment
Kindly give your valuable feedback to improve this website.