[BA 1st Sem Question Papers, Dibrugarh University, 2012, Mathematics, General]
1. Answer the following questions: 1x4=4
- The range of a real sequence may contain a complex number. (State True or False)
- The elements of a real sequence can be put in a one-one correspondence with what set?
- Every equation of odd degree has at least one real root. (State True or False)
- Write the number of positive real roots of the equation
2. Answer the following questions: 2x4=8
- Write the limit point(s) of the sequence
- Write the interval of
for which the sequence
converges.
- Find the equation whose roots are the reciprocals of the roots of the equation
- Find the other root of the equation
whose two roots being equal in magnitude but opposite in sing.
3. Find the value of 
3
3
4. Prove that every convergent sequence is bounded. 4
Or
Show that the sequence {1, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, …….}
oscillates infinitely.
5. Answer any two equations of the following: 5x2=10
- Show that the series
does not converge.
- Test the convergence of the series
- Show that a series with positive term
is convergent for
6. Solve the equation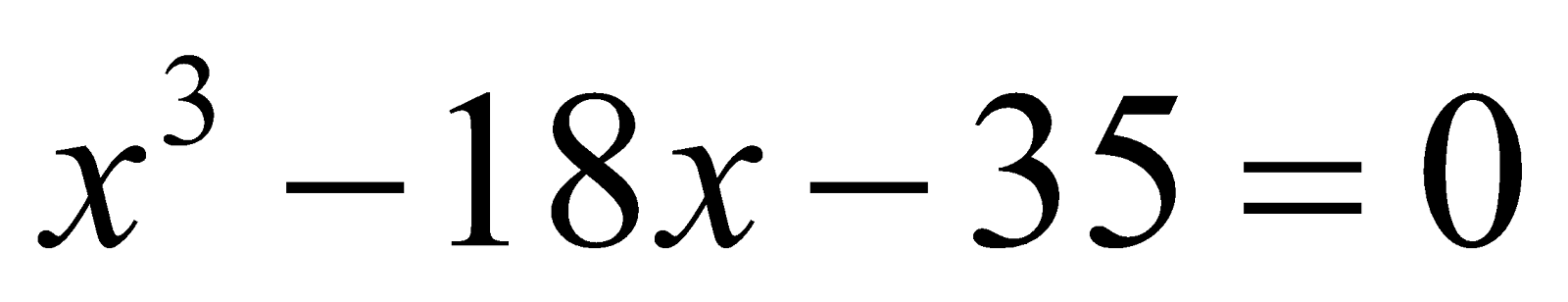 
using Cardin’s method. 10
using Cardin’s method. 10
Or
If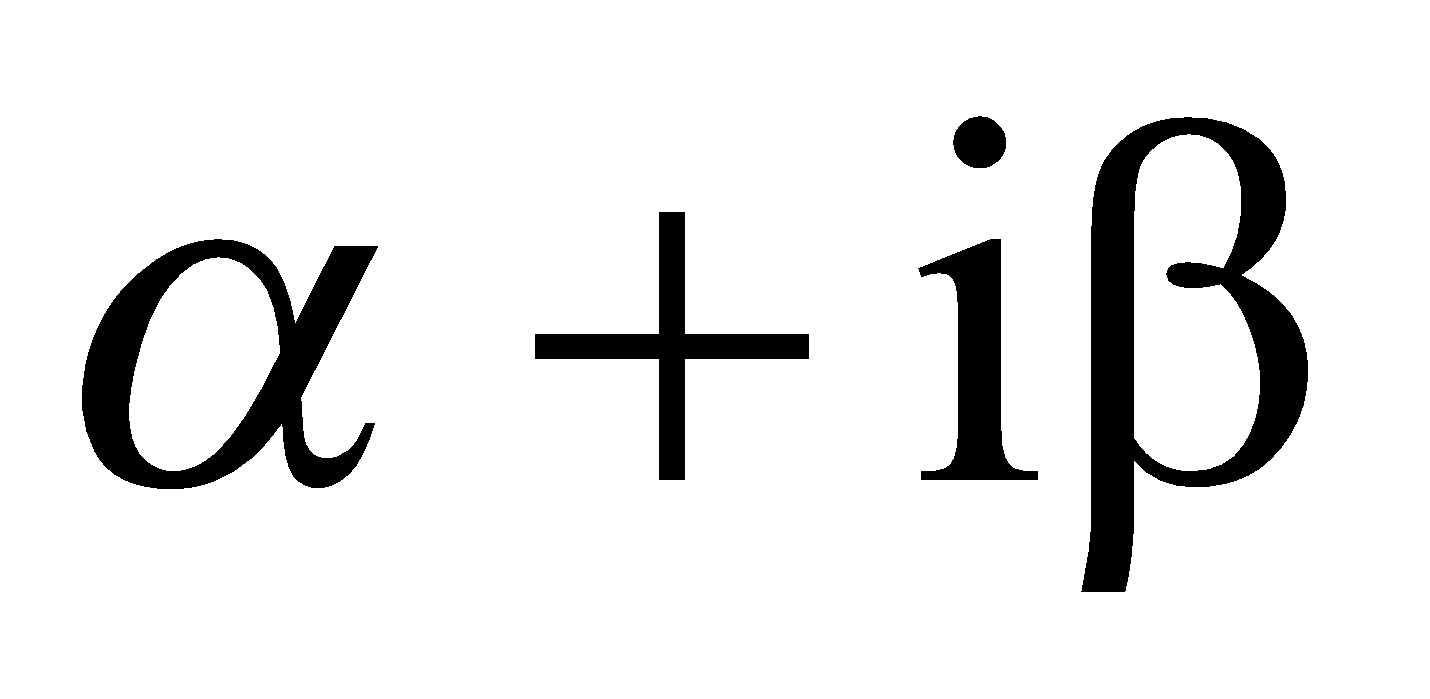 
be a root of the equation 
then show that 
is a root of the equation 
be a root of the equation then show that 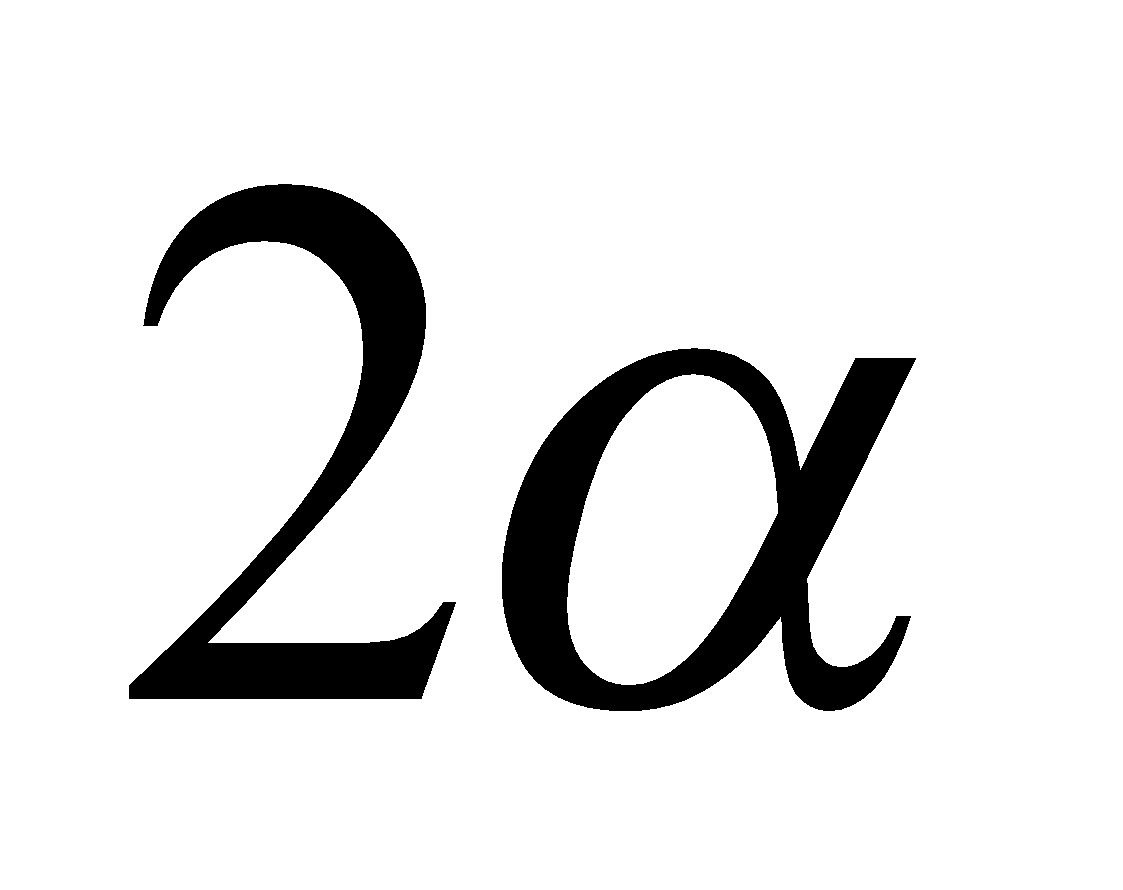is a root of the equation
7. Show that if a polynomial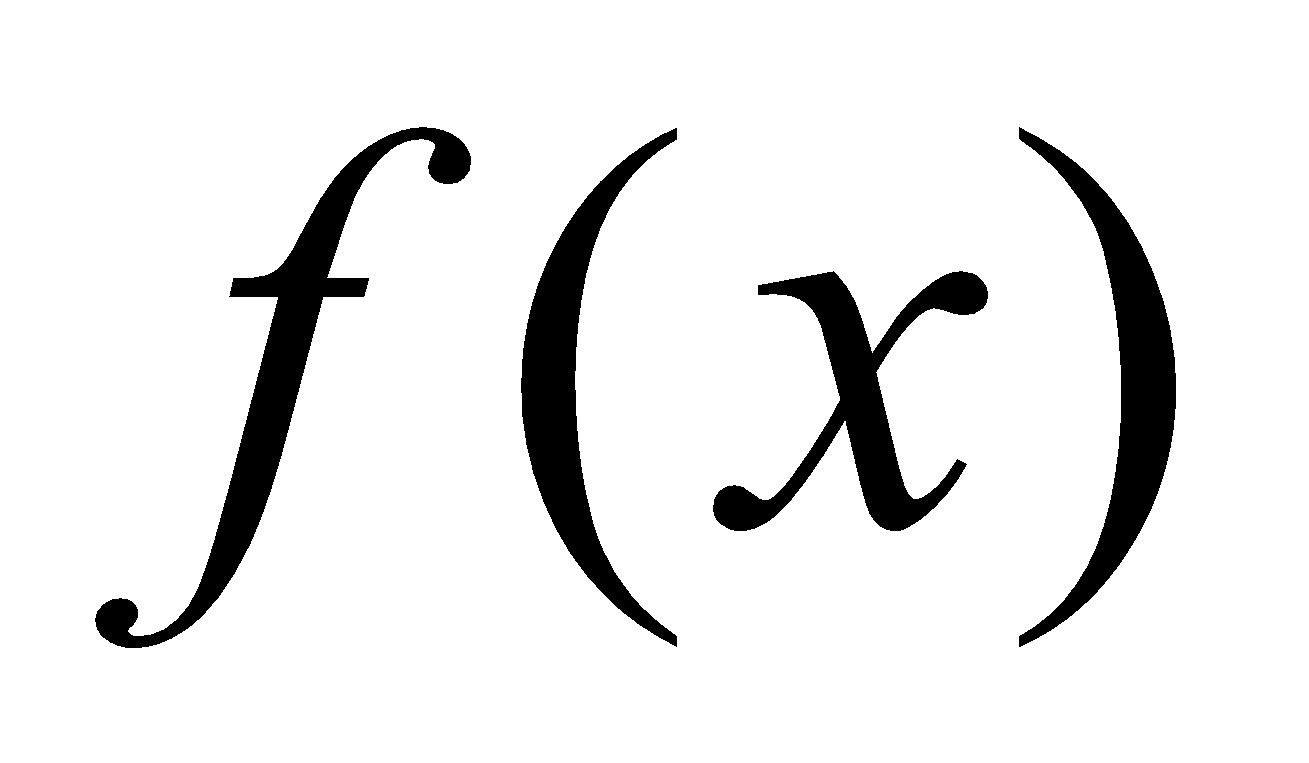 
be divided by a binomial 
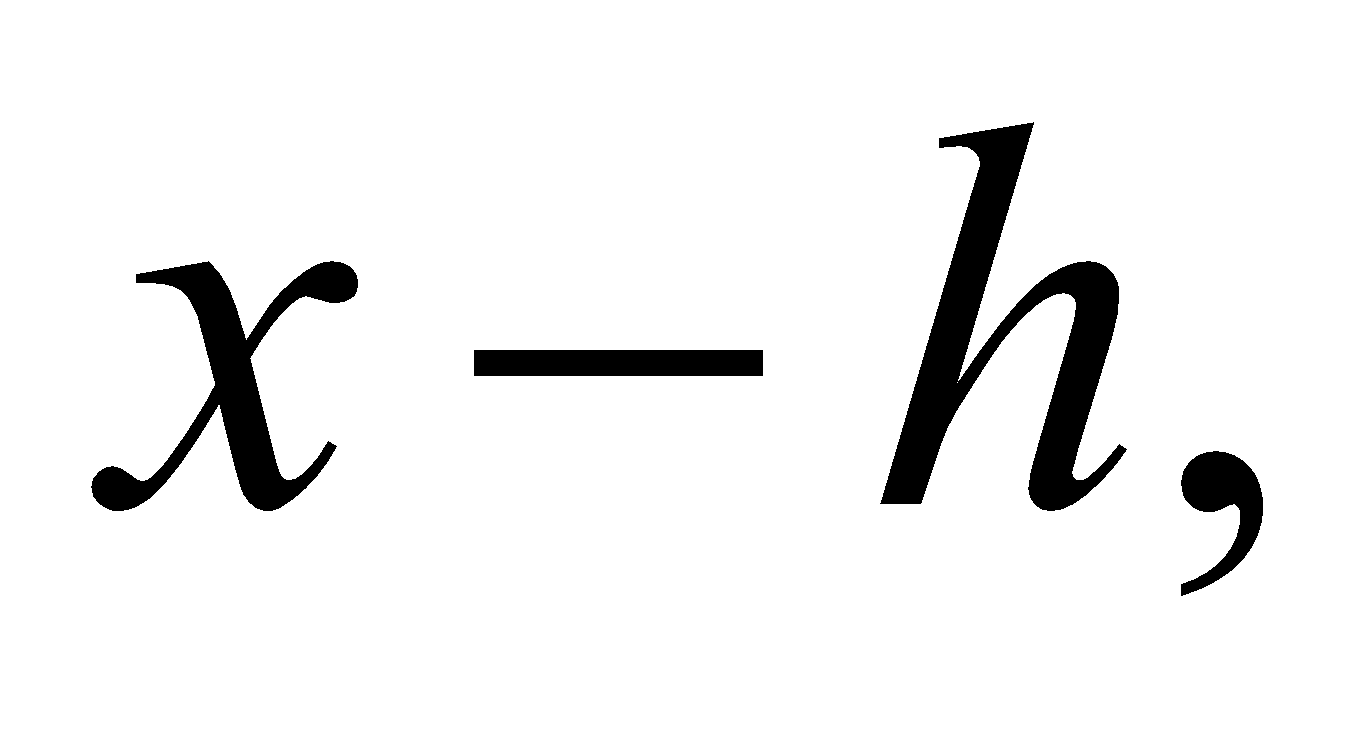then remainder is 
5
be divided by a binomial then remainder is 5
GROUP – B
(Trigonometry)
8. (a) Write the solution (s) of the equation 
1
1
(b) Write the number of values of logarithm of a complex number. 1
9. (a) Determine the value of 
(b) Write the sum of the series
. 2
10. If 
is a positive integer, then show that 5
is a positive integer, then show that 5
Or
Find the value of 
11. Show that 4
Or
Show that
12. Show that the coefficient of 
in the expansion of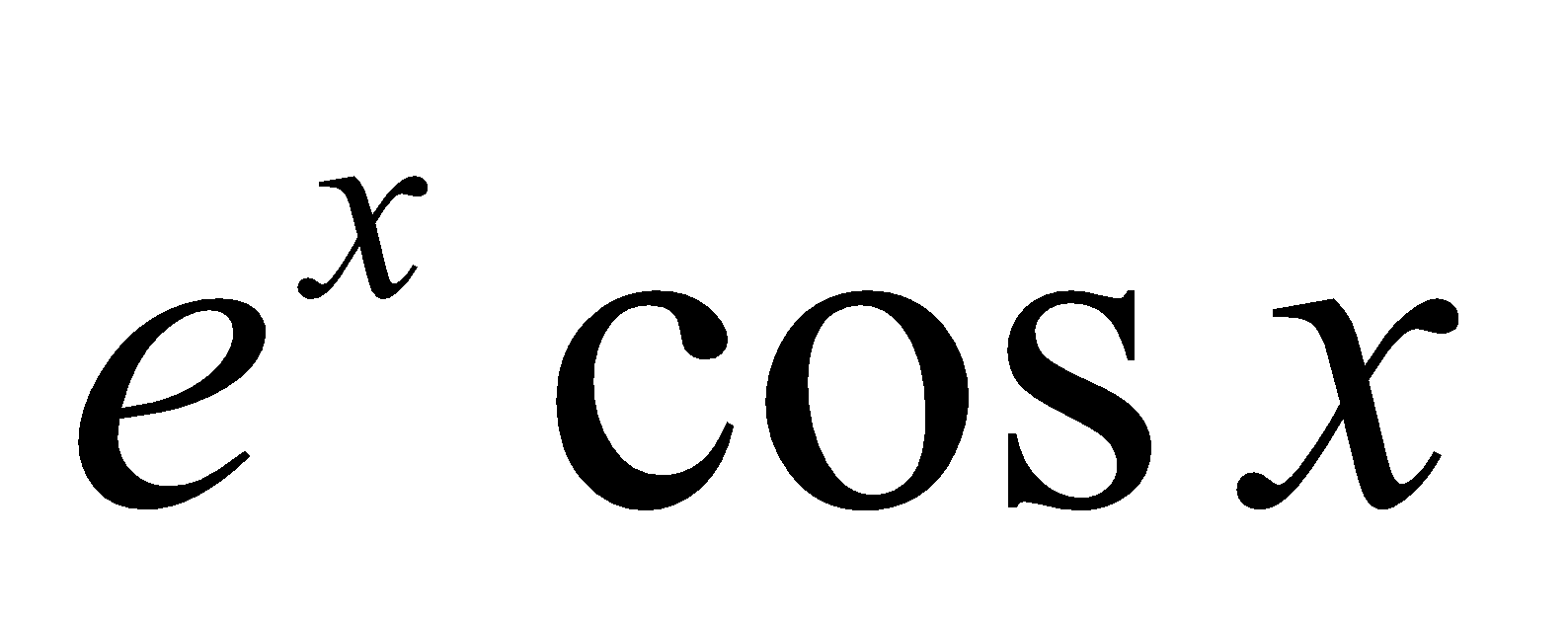 
in powers of 
is. 4
in the expansion of in powers of is. 4
13. Answer any two of the following: 3x2=6
- Find the sum to n terms the series
- Separate
into real and imaginary parts.
- Prove that
GROUP – C
(Vector Calculus)
14. (a) Find the value of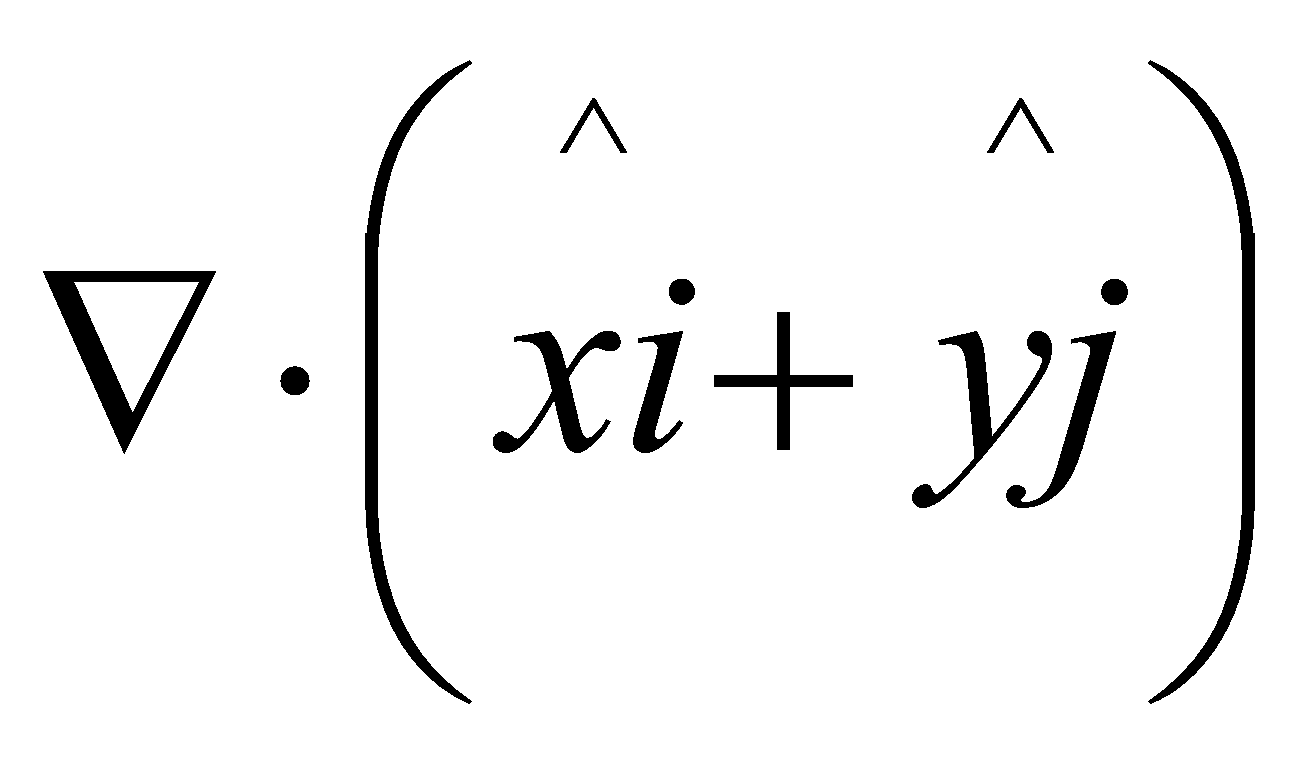 
1
1
(b) Write the definition of an irrotational vector. 1
(c) Find
, where 
2
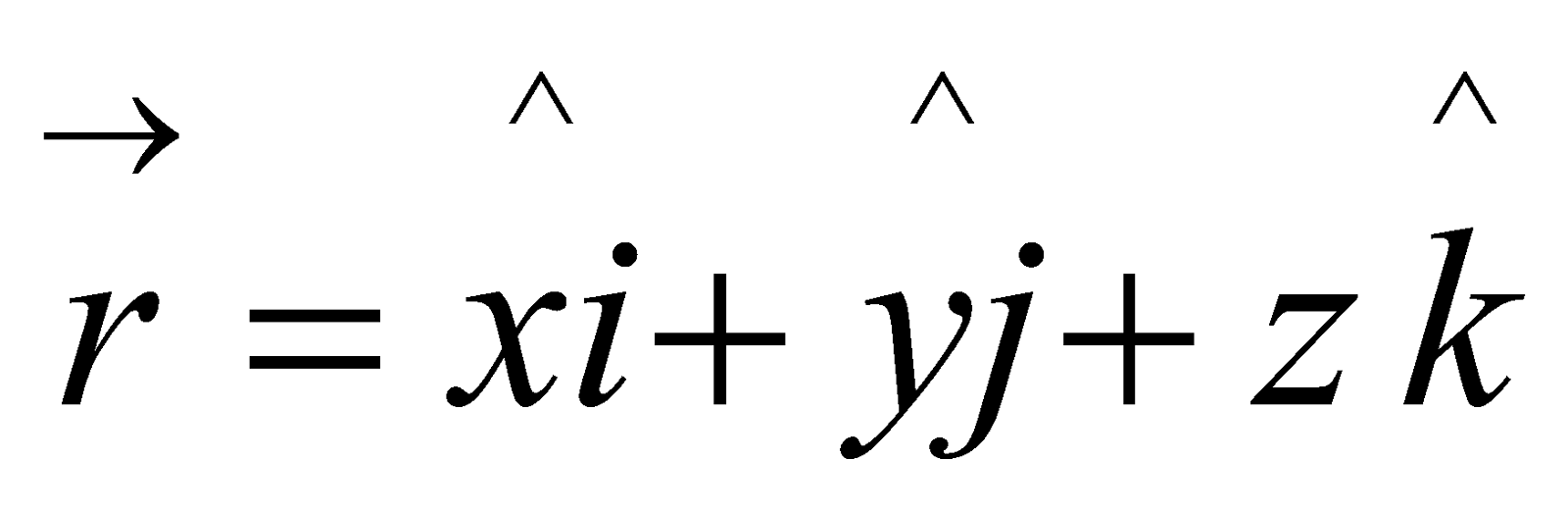, where 2
15. Prove that 
3
3
16. Answer any two of the following: 4x2=8
- Find
- Evaluate:
- Show that
is a vector perpendicular to the surface
where
is a constant.
***
Post a Comment
Kindly give your valuable feedback to improve this website.